Last time we got into some pretty heavy philosophical discussions of the physical Universe in my posting on The Foundations of Quantum Computing and laid the groundwork for how quantum computers might affect your career path in the future as a quantum computer programmer. Additionally, my hope was to reveal just how intangible the physical Universe has become thanks to 20th-century physics in order to strengthen the analogy between software in the Software Universe and matter in the physical Universe. In this posting, we shall probe a bit deeper still. Perhaps there is also a stronger tie between the Software Universe running on classical computers and the physical Universe itself. In this posting, we will examine the idea that the physical Universe may essentially be running on a large network of quantum computers. The idea of using a network of computers as a model for the behavior of the physical Universe goes back to Konrad Zuse’s Calculating Space published in 1967. In 1990, Edward Fredkin at Boston University published Digital Mechanics, in which he proposed that the physical Universe might be a cellular automaton programmed to act like physics and launched the field of digital physics. In 1998, John Wheeler stated, "it is not unreasonable to imagine that information sits at the core of physics, just as it sits at the core of a computer". Building upon his famous ”it from bit” commentary, David Chalmers of the Australian National University has summarized Wheeler’s thoughts as:
"Wheeler (1990) has suggested that information is fundamental to the physics of the universe. According to this "it from bit" doctrine, the laws of physics can be cast in terms of information, postulating different states that give rise to different effects without actually saying what those states are. It is only their position in an information space that counts. If so, then information is a natural candidate to also play a role in a fundamental theory of consciousness. We are led to a conception of the world on which information is truly fundamental, and on which it has two basic aspects, corresponding to the physical and the phenomenal features of the world".
In 2002, Seth Lloyd at MIT published The Computational Universe, in which he calculated the computing power of the entire physical Universe treated as one large quantum computer. You can read this fascinating paper at:
http://www.edge.org/3rd_culture/lloyd2/lloyd2_p2.html
Lloyd is currently working on quantum computers at MIT and is the first quantum mechanical engineer in MIT’s Mechanical Engineering department. Seth Lloyd is recognized for proposing the first technologically feasible design for a quantum computer, and recently published an excellent book that goes into greater detail on the subject Programming the Universe: A Quantum Computer Scientist Takes on the Cosmos (2006). In this book, Lloyd proposes that the physical Universe is a huge quantum computer calculating what we observe in the physical Universe. As you know, I am a true positivist at heart when it comes to software so I would prefer to say that the physical Universe behaves like a quantum computer, rather than the physical Universe actually is a quantum computer.
My hope is that over the past few postings, you have become aware of the ever-increasing importance of the concept of information in the development of physics in the 19th and 20th centuries. Beginning with the impact of Maxwell’s Demon upon thermodynamics and statistical mechanics in the 19th century, and progressing into the 20th century with the special theory of relativity and the role of the speed of information transmission in regards to the preservation of causality, and finally terminating with the role of information in quantum mechanics. As we saw our 200-pound man slowly dissolve into pure mathematics in my last posting, it seems like the physical Universe may simply consist of information in the form of mathematics. So when it comes to the physical Universe, I am, along with Roger Penrose a closet Platonist – the physical Universe seems to be made of information – mathematical information that exists even if we do not. In this worldview, we do not invent mathematics, we simply discover the mathematics that already “exists”. For a real challenge, try Roger Penrose’s The Road to Reality: A Complete Guide to the Laws of the Universe. It is a 1,099-page book just a little beyond my abilities. My one regret in life is the inadequacies of my own intellect, but I always strive for greater heights.
Although I have a strong positivist bent when it comes to software, I am much less so inclined when it comes to the actual physical Universe. My current worldview of the physical Universe is more in line with some of the non-Copenhagen interpretations of quantum mechanics which reject the extreme positivism of the Copenhagen interpretation. In The Foundations of Quantum Computing we saw that recent quantum experiments over the past 25 years have shown that photons somehow have a sense of the future, in that when approaching a two-slit screen, they seem to know in advance what lies beyond. If there are detectors that are switched on, they know to behave like particles and to go through one slit or the other. If the detectors are switched off, they know to behave like waves and to go through both slits at the same time. And in EPR experiments, quantum mechanically entangled photons seem to instantly sense what has happened to their twins, even when separated by 60 miles of space. We also discussed how the Copenhagen and Many-Worlds interpretations of quantum mechanics tried to explain these observations. Both interpretations present some rather undesirable philosophical dilemmas. In the Copenhagen interpretation, objects do not really exist until a measurement is taken, which collapses their associated wavefunctions, but the mathematics of quantum mechanics does not shed any light on how a measurement could collapse a wavefunction. And then there is the problem of an infinite regress of measuring devices highlighted by Eugene Wigner, with Wigner’s requirement for a conscious being to terminate the regress by becoming aware of an observation. In The Fabric of Reality (1997) David Deutsch rejects the extreme positivism of the Copenhagen interpretation as, borrowing a term from my youth, a cop-out. If you just don’t understand something like physical reality, it is rather easy to simply deny that it exists. Deutsch believes that physics owes us more than merely a method for calculating quantum probabilities; it owes us an explanation of how and why events actually occur. Deutsch is a strong advocate of the Many-Worlds interpretation, in which reality really does exist, but as an infinite number of realities in an infinite number of parallel universes.
So if taking a positivistic viewpoint is a cop-out, why do I do so in softwarephysics? The reason I take a positivistic approach to software in softwarephysics is that, unlike the physicists in the physical Universe, IT professionals in the Software Universe mistakenly think that they already understand the true nature of software. IT people already think that they have a TOE, a Theory of Everything, that explains what is going on when it comes to software. So why bother with all this softwarephysics? It’s all just some silly physics after all. My response to that objection is that if you think that you really know what software “really” is, then as Ayn Rand cautioned, please “check your premises”. If you keep digging deeper into software, eventually you must cross over to the hardware that runs the software, and then you get into real trouble, as we saw in my last posting as our mythical 200-pound man gradually dissolved into pure mathematics. A 200-pound bank of servers would do just the same.
Softwarephysics does not delve deeper than treating the individual characters in source code as atoms in interacting organic molecules. Each character in a line of source code is defined by 8 ASCII bits, which are the equivalent of 8 electrons in 8 electron shells, with each electron in a spin-up↑ or spin-down ↓ state:
discountedTotalCost = (totalHours * ratePerHour) - costOfNormalOffset;
C = 01000011 = ↓ ↑ ↓ ↓ ↓ ↓ ↑ ↑
H = 01001000 = ↓ ↑ ↓ ↓ ↑ ↓ ↓ ↓
N = 01001110 = ↓ ↑ ↓ ↓ ↑ ↑ ↑ ↓
O = 01001111 = ↓ ↑ ↓ ↓ ↑ ↑ ↑ ↑
Our challenge as IT professionals is to arrange these characters (atoms) into complex patterns in the face of the second law of thermodynamics that demands that the total amount of entropy or disorder in the Universe must always increase whenever a change is made. This is due to the fact that for a given chunk of software, there are nearly an infinite number of incorrect versions or microstates of the software, and very few correct versions or microstates of the same chunk of software. For example, late last night I was building out WebSphere 6.1 on 4 WebSphere servers in one of our Unix server farms. After about 4 hours of work, I was just about to finish up by federating the 4 new WebSphere 6.1 nodes that I had just created into a new WebSphere 6.1 Cell. The Unix command that I had been given by our WebSphere Engineering team to do the federation was 39 bytes or characters long and contained two characters or atoms in the wrong quantum states. The characters were supposed to be “ob”, but were “sx” instead.
o = 01101111 = ↓↑↑↓↑↑↑↑
b = 01100010 = ↓↑↑↓↓↓↑↓
s = 01110011 = ↓↑↑↑↓↓↑↑
x = 01111000 = ↓↑↑↑↑↓↓↓
When I ran the command, I had that sinking IT feeling familiar to all, as all sorts of errors scrolled by in a blur. The command I was given was trying to federate the new nodes into the wrong Cell! Luckily, a WebSphere security setting at the other Cell prevented the federation. Otherwise, I would never have even noticed the problem. And while I was in the middle of trying to figure out why I had just seen 300 lines of error messages scroll by, I was paged into a conference call to try to figure out why one of the WebSphere Datasources on a different appserver was getting slow response time from one particular Oracle database. At the same time, an Offshore teammate in India instant messaged me with a question about another install that was not going so well. I finally paged out my WebSphere Engineering contact, and he spotted the typo, so when I ran the command again, everything worked OK. Such is life in IT. Fortunately, I have softwarephysics to help me keep my sanity.
Softwarephysics stops at the level of individual characters in software because, from a positivistic point of view, it provides the basis for a useable effective theory of software behavior sufficient to help IT people perform their jobs in a more effective manner. This is essentially what chemists do. As we have seen, chemistry is simply a very useful effective theory of matter that is an approximate extension of quantum mechanics and QED at a sufficiently high level to hide the intricacies of the underlying quantum mechanics and QED. Similarly, as I pointed out in So Why Are There No Softwarephysicists? economists adopt an equivalent strategy when dealing with the virtual substance we call money. It is much easier to treat money as an actual substance that “really” exists, as opposed to a large collection of bits on a vast network of computers. I am frequently surprised at just how “real” money is for most people when, after all, it is just information encoded in the spin states of a large number of iron atoms on disk drives. As I previously mentioned, I am also amazed that, after all this time, there still is no effective theory of software behavior in computer science beyond softwarephysics. I would venture to say that the economic impact of software in the modern world is just as great as the invention of money. Yet, there are no softwarephysicists to speak of. It seems strange that one can receive a Nobel prize for a macroeconomic theory that produces an improved model for the behavior of the virtual substance we call money, but not so for a similar model for the virtual substance we call software. So in softwarephysics, I strive to keep the analysis at a sufficiently high level to still prove useful to the average IT professional, just as physicists still use Newtonian mechanics to launch space probes to the outer planets and not the general theory of relativity. Going deeper would only get us into trouble. Softwarephysicists have one advantage over physicists, we know the predicament that lies behind the curtain and, at this early stage of softwarephysics theory, we can safely afford the luxury to ”Pay no attention to that man behind the curtain”.
The Transactional Interpretation of Quantum Mechanics
Before we leave this topic, I would like to introduce you to my favorite interpretation of quantum mechanics called the Transactional Interpretation, developed by John Cramer at the University of Washington in 1986.
In my humble opinion, the Transactional Interpretation comes with far fewer philosophical problems than the other interpretations of quantum mechanics, and all IT people should easily relate to it because the Transactional Interpretation runs along the lines of the TCP/IP protocol. Cramer does not exactly mention TCP/IP in his paper, but all the steps are there nonetheless. You can download his original paper at:
http://faculty.washington.edu/jcramer/TI/tiqm_1986.pdf
Before I delve further into the Transactional Interpretation of quantum mechanics, let’s review the TCP/IP protocol first. Below is a quick refresher available in cyberspacetime from the Wikipedia. Please note the similarity between TCP/IP and Richard Feynman’s "path integral" or "sum over histories" approach to quantum mechanics and QED in that the packets in a message can take different paths through cyberspacetime to arrive at their ultimate destination.
The Internet Protocol (IP) works by exchanging groups of information called packets. Packets are short sequences of bytes consisting of a header and a body. The header describes the packet's destination, which routers on the Internet use to pass the packet along, generally in the right direction, until it arrives at its final destination. The body contains the application data.
In cases of congestion, the IP can discard packets, and, for efficiency reasons, two consecutive packets on the Internet can take different routes to the destination. Then, the packets can arrive at the destination in the wrong order.
The TCP software libraries use the IP and provide a simpler interface to applications by hiding most of the underlying packet structures, rearranging out-of-order packets, minimizing network congestion, and re-transmitting discarded packets. Thus, TCP very significantly simplifies the task of writing network applications.
TCP is the transport protocol that manages the individual conversations between web servers and web clients.
TCP provides connections that need to be established before sending data. TCP connections have three phases:
1. connection establishment
2. data transfer
3. connection termination
Connection establishment
To establish a connection, TCP uses a three-way handshake. Before a client attempts to connect with a server, the server must first bind to a port to open it up for connections: this is called a passive open. Once the passive open is established, a client may initiate an active open. To establish a connection, the three-way (or 3-step) handshake occurs:
1. The active open is performed by the client sending a SYN to the server.
2. In response, the server replies with a SYN-ACK.
3. Finally, the client sends an ACK back to the server.
At this point, both the client and server have received an acknowledgment of the connection.
Data transfer
There are a few key features that set TCP apart from User Datagram Protocol:
Ordered data transfer - the destination host rearranges according to sequence number.
Retransmission of lost packets - any cumulative stream not acknowledged will be retransmitted. Discarding duplicate packets
Error-free data transfer
Flow control - limits the rate a sender transfers data to guarantee reliable delivery. When the receiving host's buffer fills, then next acknowledgement contains a 0 in the window size, to stop transfer and allow the data in the buffer to be processed.
Congestion control - sliding window
Connection termination
The connection termination phase uses, at most, a four-way handshake, with each side of the connection terminating independently. When an endpoint wishes to stop its half of the connection, it transmits a FIN packet, which the other end acknowledges with an ACK. Therefore, a typical tear down requires a pair of FIN and ACK segments from each TCP endpoint...
In Cramer’s Transactional Interpretation, when two electrons interact, they do so by first establishing a socket connection using the 3-step handshake of TCP/IP. They then exchange a number of packets of information “sufficient to satisfy all of the quantum boundary conditions [E=h(nu) and various conservation laws], at which point the transaction is completed.”
To fully appreciate Cramer’s interpretation, we need to review a little more physics. First of all, we need to worry a bit about the concept of reality in electrodynamics. As we saw in my last posting, the concept of reality has grown rather murky, especially when it comes to the interpretations of the quantum world. In the words of Max Planck ”Great caution must be exercised in using the word, real” and of Poincare, ”What this world consists of, we cannot say or conjecture, we can only conjecture what it seems, or might seem to be to the minds not too different from ours”.
Recall that in the 19th century, there was great reluctance on the part of some physicists, especially the French, in accepting Michael Faraday’s concept of electric and magnetic fields as being “real”. Some physicists thought that these fields were merely a convenient mathematical device and not something that was actually “real”. Similarly, in 1864 when James Clerk Maxwell demonstrated that electromagnetic waves could propagate in free space, at least mathematically, with the wave equation:
∂²Ey = με ∂²Ey
─── ───
∂x² ∂t²
many physicists were skeptical until 1886 when Heinrich Hertz was able to demonstrate the creation and detection of electromagnetic radio waves. But even with the findings of Hertz, all that we know is that when we jiggle electrons on one side of a room, we make electrons on the other side of the room jiggle as well. Does that mean that there is an electromagnetic wave involved? Fortunately, we can refine our experiment with the aid of a microwave oven. Open your microwave oven and remove the rotating platter within. Now get a small Espresso coffee cup and commit the ultimate Starbucks sin, heat a small cup of cold coffee in the microwave at various positions within the oven. What you will find is that at some locations in the oven, the coffee gets quite hot, and at others, it does not. So what is happening? In the classical electrodynamics of Maxwell, there is a microwave standing wave within the oven. If you are fortunate enough to place your Espresso cup at a point in the microwave oven where the standing wave is intense, the coffee will heat up quite nicely. If you place the Espresso cup at a node point where the standing microwave is at a minimum, the coffee will not heat up as well. That is why they put the rotating platter in the microwave oven. By rotating objects in the oven, the objects pass through the hot and cold spots of the standing electromagnetic microwave and are evenly heated. So this is pretty convincing evidence that electromagnetic waves really do exist, even for a positivist.
But now let us look at this same experiment from the point of view of quantum mechanics and QED. If you have been paying attention, you might have noticed that our microwave oven is simply a physical implementation of the famous “particle in a box” we discussed previously. The only difference is that we are using microwave photons in our box instead of electrons. Now according to quantum mechanics and QED, the reason that the coffee in the Espresso cup got hotter in some spots and less hot in others is that the probability of finding microwave photons at certain spots in the oven is greater than finding them at other spots based upon the square of the amplitude of the wavefunctions Ψ of the photons. But remember, in the Copenhagen interpretation of quantum mechanics, the wavefunctions Ψ of particles and photons are not “real” waves, they are only probability waves – just convenient mathematical constructs that don’t “really” exist, similar to the electromagnetic waves of the mid-19th century that did not “really” exist either.
But in Cramer’s Transactional Interpretation of quantum mechanics, the wavefunctions Ψ of particles and photons really do exist. For a physics student new to quantum mechanics, this is truly a comforting idea. Before they teach you about quantum mechanics, you go through a lengthy development of wave theory in courses on classical electrodynamics, optics, and differential equations. In all these courses, you only deal with waves that are mathematically real, meaning that these waves have no imaginary parts using the imaginary number i where i2 = -1. But in your first course on quantum mechanics, you are introduced to Schrödinger’s equation:
-ħ² ∂²Ψ = iħ ∂Ψ
── ── ──
2m ∂x² ∂t
and learn that generally, the wavefunction solutions to Schrödinger’s equation contain both real and imaginary parts containing the nasty imaginary number i. Consequently, the conventional wisdom is that the wavefunction solutions to Schrödinger’s equation cannot really exist as real tangible things. They must just be some kind of useful mathematical construct. However, in the same course, you are also taught about Davisson and Germer bouncing electrons off the lattice of a nickel crystal and observing an interference pattern, so something must be waving! I would venture to suggest that nearly all students new to quantum mechanics initially think of wavefunctions as real waves waving in space. Only with great coaxing by their professors do these students “unlearn” this idea with considerable reluctance.
As we saw previously, the imaginary parts of wavefunctions really bothered the founding fathers of quantum mechanics too. Recall that in 1928, Max Born came up with the clever trick of multiplying the wavefunctions Ψ by their complex conjugates Ψ* to get rid of the imaginary parts. To create the complex conjugate of a complex number or function, all you have to do is replace the imaginary number i with –i wherever you see it. According to Born’s conjecture, the probability of things happening in the quantum world are proportional to multiplying the wavefunction by its complex conjugate Ψ*Ψ. Mathematically, this is the same thing as finding the square of the amplitude of the wavefunction. Now in my last posting, I mentioned how Richard Feynman pointed out that instead of thinking of positrons having negative energy, you could also think of positrons as regular electrons with positive energy moving backwards in time by shifting the position of the “-“ sign in the wavefunction of a positron. But that is just the same thing as using the complex conjugate Ψ* of an electron wavefunction for a positron. So mathematically, we can think of the complex wavefunction of a particle Ψ* as the wavefunction of the particle moving backwards in time. Cramer suggests that Born’s idea of Ψ*Ψ representing the probability of a quantum event is not just a mathematical trick or construct, rather it is the collision of an outgoing “retarded” wave Ψ moving forwards in time with an incoming Ψ* “advanced” wave moving backwards in time. The terms “retarded” and “advanced” wave go back to some work done by John Wheeler and Richard Feynman in 1945 in regards to the self-energy of electrons which never quite caught on. In the discussion below, just remember that “retarded” means moving forwards in time and “advanced” means moving backwards in time. Recall that quantum mechanics was initiated in 1900 by Max Planck with the mathematical trick of conjecturing that the charged particles in the walls of an oven could only oscillate with fixed quantized frequencies. In 1905, Einstein proposed that Planck’s idea was not a mathematical trick at all - light “really” could be considered as a stream of particles that we now call photons with quantized energies. Similarly, John Cramer suggests that we fess up and finally accept the idea that wavefunctions are just as “real” as anything else in this very strange Universe that we live in. There is a famous quote by Steven Weinberg in The First Three Minutes (1977) that comes to mind “Our mistake is not that we take our theories too seriously, but that we do not take them seriously enough. It is always hard to realize that these numbers and equations we play with at our desks have something to do with the real world”.
There is one other technical detail. If you compare Maxwell’s wave equation for the electric field component E of an electromagnetic wave with Schrödinger’s equation, you will notice that in addition to containing the imaginary number i, Schrödinger’s equation uses the first derivative with respect to time of Ψ rather than the second derivative with respect to time. These terms both appear on the right side of the wave equations. Recall that the first derivative of a curvy line is just the slope of the line at each point along the line and that the second derivative is just the curvature of the line at each point along the line. Now it turns out that this makes a difference. In order to have an “advanced” wave solution moving backwards in time, the wave equation needs that second order derivative term and not a first-order derivative. But as I pointed out previously, back in 1926 Schrödinger did not take into account relativistic effects. His equation contains the mass m of the particle in question, and we know that spells trouble if E = mc2. However, when you use a version of the Schrödinger wave equation that has been corrected for relativistic effects, you can have “advanced” wavefunction solutions moving backwards in time.
But everybody loves the Schrödinger equation for its comparative simplicity. The good news is that if you take the complicated relativistic version of Schrödinger’s equation, and throw out the math terms that only relate to objects moving near the speed of light, you end up with two very good approximate wave equations. The first one is the standard Schrödinger equation for particles moving forwards in time as a retarded wave:
-ħ² ∂²Ψ = iħ ∂Ψ
── ── ──
2m ∂x² ∂t
And the second equation is just the complex conjugate of the above equation that we obtain by simply sticking a “-“ sign in front of the imaginary number i. This equation only has “advanced” wavefunction solutions moving backwards in time:
-ħ² ∂²Ψ = -iħ ∂Ψ
── ── ──
2m ∂x² ∂t
Details of the Transactional Interpretation of Quantum Mechanics
So let us examine Cramer’s Transactional Interpretation of quantum mechanics in some detail by analyzing the interaction of two electrons as outlined in his paper. However, let us also throw in the equivalent TCP/IP steps of the interaction as well.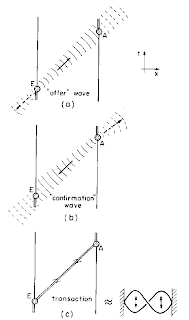
Figure 4 – From John Cramer’s paper on the Transactional Interpretation (click to enlarge)
The figure above is Figure 4 from Cramer’s paper and depicts the interaction of an emitting client electron E and an absorbing server electron A. All of the quotes that follow are from John Cramer’s paper.
1. An emitting client electron E sends out a SYN to an absorbing server electron A. Cramer calls the SYN an “offer wave” F1(r,t ≥T1) that is a retarded wave sent forwards in time (moving up into the future of the spacetime plot of Figure 4 step a). The emitting client electron E also sends the SYN out as an advanced wave G1(r,t ≤T) going backwards in time (moving down and into the past in the spacetime plot of Figure 4 step a).
”In the first pseudo-sequential step (1) the emitter located at (R1,T1), sends out a waves F1(r,t≥T1) and G1(r,t≤T ) (which can be of spherical or more complicated form) in all possible spatial directions.”
2. When the absorbing server electron A receives the SYN (offer wave), it responds with a SYN-ACK (confirmation wave) that is sent backwards in time (moving down into the past in the spacetime plot of Figure 4 step b). The SYN-ACK (confirmation wave) therefore arrives back at the client emitter electron E at the same time that the client electron E sends out the initial SYN (offer wave). Remember this is quantum mechanics!
”In step (2) the absorber located at (R2,T2), receives the attenuated retarded wavefront F1(R2,T2) and is stimulated to produce a response wave G2(r,t) which has an initial amplitude proportional to the local amplitude of the incident wave which stimulated it”:
3. The client emitter electron E then sends out a final ACK to establish the connection between the client emitter electron E and the absorbing server electron A (Figure 4 step c).
”In step (3) the advanced wave G2 propagates back to the locus of emission, at which it has an amplitude which is proportional to its initial amplitude F1(R2,T2) multiplied by the attenuation which it has received in propagating from the absorption locus to the emission locus. But the advanced wave G2 travels across the same spatial interval and through the same attenuating media encountered by F1, but in reverse. For this reason, the unit amplitude wave g2(R1,T1) arriving back at the emitter has an amplitude which is proportional to F1*(R2,T2), the time reverse of the retarded wave which reached the absorber….
This means that the advanced "confirmation" or "echo" wave which the emitter receives from the absorber as the first exchange step of the incipient transaction is just the absolute square of the initial "offer" wave, as evaluated at the absorber locus. The significance of this Ψ Ψ* echo and its relation to Born's probability law will be discussed in Section 3.8 below.”
Once the connection has been firmly established, the two electrons then transmit sufficient packets of data back and forth to:
”In step (4) the emitter responds to the "echo" and the cycle repeats until the response of the emitter and absorber is sufficient to satisfy all of the quantum boundary conditions [E=h(nu) and various conservation laws], at which point the transaction is completed. Even if many such echoes return to the emitter from potential absorbers, the quantum boundary conditions can usually permit only a single transaction to form.”
Figure 4 step c depicts this exchange of packets as a standing wave between the emitter E and absorber A like the standing wave in our microwave oven.
In the words of the Wikipedia, the TCP/IP transaction is terminated
”When an endpoint wishes to stop its half of the connection, it transmits a FIN packet, which the other end acknowledges with an ACK. Therefore, a typical tear down requires a pair of FIN and ACK segments from each TCP endpoint.”
Cramer summarizes all this as:
”This, in a simplified one-dimensional form which will be expanded below, is the emitter-absorber transaction. The emitter can be considered to produce an "offer" wave F1 which travels to the absorber. The absorber then returns a "confirmation" wave to the emitter and the transaction is completed with a "handshake" across space-time. To an observer who had not viewed the process in the pseudo-time sequence {footnote 14} employed in the above discussion, there is no radiation before T1 or after T2 but a wave traveling from emitter to absorber. This wave can be reinterpreted as a purely retarded wave because its advanced component G2, a negative energy wave traveling backwards in time from absorber to emitter, can be reinterpreted as a positive energy wave traveling forward in time from emitter to absorber, in one-to-one correspondence with the usual description {footnote 15}.”
”To summarize the transaction model, the emitter produces a retarded offer wave (OW) which travels to the absorber, causing the absorber to produce an advanced confirmation wave (CW) which travels back down the track of the OW to the emitter. There the amplitude is CW1~|OW2|2, where CW1 is evaluated at the emitter locus and OW2 is evaluated at the absorber locus. The exchange then cyclically repeats until the net exchange of energy and other conserved quantities satisfies the quantum boundary conditions of the system, at which point the transaction is complete. Of course the pseudo-time sequence {footnote 14} of the above discussion is only a semantic convenience for describing the onset of the transaction. An observer, as in the simpler plane wave case, would perceive only the completed transaction which he could reinterpret at the passage of a single retarded (i.e., positive energy) photon traveling at the speed of light from emitter to absorber {footnote 15}.”
In the remainder of Cramer’s paper, he explains how the Transactional Interpretation easily explains all of the apparent paradoxes of quantum mechanics. As we have seen, there is actual experimental evidence that electrons and photons seem to “know” in advance what they will encounter on the other side of a double-slit experiment. This is easily explained by the Transactional Interpretation. The electrons or photons send out retarded waves into the future which interact with whatever lies beyond the slits. If there are detectors that are turned on, the retarded waves interact with them, if there are no detectors, the waves interact with some electrons on a projection screen instead. In either case, an advanced wave is sent backwards in time from the detectors or the projection screen to the point of origin of the electrons or photons so that they “know” how to behave before they get to the two-slit screen.
So here are your options. You should review them in terms of an “explanation” for quantum mechanics, rather than as a way of performing quantum mechanical calculations because all the interpretations of quantum mechanics use the very same mathematics. The question is, what is the math trying to tell us?
1. The Copenhagen interpretation – Absolute reality does not exist, but there are an infinite number of potential realities. When conscious observers come along, the Universe collapses into reality when observed. So it is never safe to turn your back on the Universe because you never know what it might be up to behind your back while you are not looking! The Copenhagen interpretation solves the age-old question of, “If a tree falls in the forest, and nobody hears it, does it make a sound?”, with, “Of course not, because there is no tree and there is no forest!”. So the Copenhagen interpretation does not go very far as an explanation of quantum mechanics. In fact, you could explain just about anything with a similar argument.
2. The Many-Worlds interpretation – Absolute reality really does exist, but it is spread across an infinite number of realities in an infinite number of parallel universes. This is more of an explanation of quantum mechanics than the Copenhagen interpretation, but it comes with the high cost of a large amount of real estate.
3. The Transactional Interpretation - There is only one reality and it “really” does exist. The only thing we have to contend with is the idea of the future sending waves back into the past. But we already have experimental evidence that this really happens!
As you can see, the Transactional Interpretation comes with much less philosophical baggage than either the Copenhagen or Many-Worlds interpretations. The main stumbling block to the Transactional Interpretation is the idea of things in the future sending advanced waves back into the past. But this is really not much of a stumbling block because nobody really understands the true nature of time anyway. For most people, time seems to flow from the past into the future as a continuous series of “Nows”. But in our discussions of the special theory of relativity, we saw that there is no absolute “Now” shared by all. My “Now” could be your “Past” and somebody else’s “Future”. In fact, all of the effective theories of physics, with perhaps the exception of the second law of thermodynamics, could care less about the apparent flow of time from the past into the future. These theories work just as well going backwards in time as going forwards in time. And we have no device that actually measures this flow of time that we all seem to sense. Clocks do not measure the rate of the flow of time, they measure an amount of time, just as a ruler measures an amount of space. Only a speedometer can measure our rate of flow through space, and we have no equivalent device for time. As we saw in our discussion of the special theory of relativity, everybody measures the flow of time in spacetime as one hour per hour. So we should not get too squeamish about things sending advanced waves backwards in time. After all, QED, the queen of physics, freely uses the idea of positrons moving backwards in time.
So why is John Cramer’s Transactional Interpretation of quantum mechanics not celebrated with the same intensity as the Copenhagen and Many-Worlds interpretations? In a future posting, I will discuss Richard Dawkins’ concept of memes and the tyranny of self-reproducing information (SRI) as it relates to the suppression of new ideas. For now, let us just say that the Transactional Interpretation is stuck at about stage 1.5 of the life-cycle for all new theories:
1. First it is ignored
2. Then it is wrong
3. Then it is obvious
4. Then somebody else thought of it 20 years earlier!
So be patient. It might take another 30 years. At this very moment, John Cramer is trying to prove that the commonly held view that you cannot send information faster than the speed of light might be wrong. In my last posting, we discussed how recent EPR experiments have revealed that for two quantum mechanically entangled photons, measuring the polarization of one photon can immediately affect the polarization of the other photon, even when the photons are separated by 60 miles. But the conventional thinking is that you cannot instantly send a message in this manner because the sender and receiver each only measure various photon polarizations and only realize that there is a correlation when they come together and compare notes. But in the Transactional Interpretation, the receiver is communicating with the sender using advanced waves sent backwards in time, and that is why the measurement of one polarization seems to immediately affect the other polarization. So John Cramer has come up with a laboratory set-up of an EPR experiment that could be used to apparently send an information containing message instantly from one location to another by essentially using the advanced waves moving backwards in time. That alone would be enough for a Nobel Prize, but Cramer has an even grander plan in store. He has the design for another EPR experiment that would allow the receiver to receive a message 50 microseconds before it was sent by the sender, demonstrating retro-causal signaling - a message from the future arriving in the present! If that should happen, a future Chairman of the Norwegian Nobel Committee might rescind his Prize before it is even awarded. After all, Einstein never received the Nobel Prize for the theory of relativity either. For details on these fascinating ongoing experiments go to:
http://faculty.washington.edu/jcramer/NLS/NL_signal.htm
If you would care to read more about John Cramer’s Transactional Interpretation of quantum mechanics and how it compares to some of the other popular interpretations, try John Gribbin’s Schrödinger’s Kittens and the Search for Reality (1995). Another interesting source is The Ghost in the Atom (1986) edited by Davies and Brown which is a compilation of BBC interviews with many of the key players of 20th-century quantum mechanics and their opinions of the various interpretations of quantum mechanics.
Next time we will wrap up the portion of softwarephysics that deals with physics by introducing another great achievement of 20th-century physics, chaos theory, and use it and all of the previous topics in softwarephysics to finally frame the fundamental problem of software.
Comments are welcome at scj333@sbcglobal.net
To see all posts on softwarephysics in reverse order go to:
https://softwarephysics.blogspot.com/
Regards,
Steve Johnston