In this post, I would like to discuss a possible new physical law of the Universe that should be of interest to all who have been following this blog on softwarephysics because it generalizes the concept of Universal Darwinism into a new physical law of the Universe. It is called the Law of Increasing Functional Information and is outlined in the paper below:
On the roles of function and selection in evolving systems
https://www.pnas.org/doi/epdf/10.1073/pnas.2310223120
and is also described in the YouTube video below:
Robert M. Hazen, PhD - The Missing Law: Is There a Universal Law of Evolving Systems?
https://youtu.be/TrNf62IGqM8?t=2114
The paper explains that four branches of classical 19th-century physics nearly explain all of the phenomena of our everyday lives:
1. Newton's laws of motion
2. Newton's law of gravitation
3. The classical electrodynamics of Maxwell and many others
4. The first and second laws of thermodynamics of James Prescott Joule and Rudolph Clausius
The authors explain that all of the above laws were discovered by the empirical recognition of the "conceptual equivalences" of several seemingly unrelated physical phenomena. For example, Newton's laws of motion arose from the recognition that the uniform motion of a body along a straight line and at a constant speed was conceptually equivalent to the accelerated motion of a body that is changing speed or direction if the concepts of mass, force and acceleration were related by three physical laws of motion. Similarly, an apple falling from a tree and the Moon constantly falling to the Earth in an elliptical orbit were also made to be conceptually equivalent by Newton's law of gravitation. Later, the many disparate phenomena of electricity and magnetism were made conceptually equivalent by means of Maxwell's equations. Finally, the many phenomena of kinetic, potential and heat energy were made conceptually equivalent by means of the first and second laws of thermodynamics.
The authors then go on to wonder if there is a similar conceptual equivalence for the many seemingly disparate systems that seem to evolve over time such as stars, atomic nuclei, minerals and living things. As a softwarephysicist, I would add software to that list as well. Is it possible that we have overlooked a fundamental physical law of the Universe that could explain the nature of all evolving systems? Or do evolving systems simply arise as emergent phenomena from the
four branches of classical physics outlined above? The authors point out that the very low entropy of the Universe immediately following the Big Bang could have taken a direct path to a very high-entropy patternless Universe without producing any complexity within it at all while still meticulously following all of the above laws of classical physics. But that is not what happened to our Universe. Something got in the way of a smooth flow of free energy dissipating from low to high entropy, like the disruption caused by many large rocks in a mountain stream, allowing for the rise of complex evolving systems far from thermodynamic equilibrium to form and persist.
Some have tried to lump all such evolving systems under the guise of Universal Darwinism. In this view, the Darwinian processes of inheritance, innovation and natural selection explain it all in terms of the current laws of classical physics. But is that true? Are we missing something? The authors propose that we are because all evolving systems seem to be conceptually equivalent in three important ways and that would suggest that there might exist a new underlying physical law guiding them all.
1. Each system is formed from numerous interacting units (e.g., nuclear particles, chemical elements, organic molecules, or cells) that result in combinatorially large numbers of possible configurations.
2. In each of these systems, ongoing processes generate large numbers of different configurations.
3. Some configurations, by virtue of their stability or other “competitive” advantage, are more likely to persist owing to selection for function.
The above is certainly true of software source code. Software source code consists of a huge number of interacting symbols that can be combined into a very large number of possible configurations to produce programs.

Figure 1 – Source code for a C program that calculates an average of several numbers entered at the keyboard.
There are also millions of programmers, and now LLM (Large Language Models) like Google Bard or OpenAI GPT-4, that have been generating these configurations over the past 82 years, or 2.6 billion seconds, ever since Konrad Zuse first cranked up his Z3 computer in May of 1941. And as programmers work on these very large configurations, they are constantly discarding "buggy" configurations that do not work. But even software that "works" just fine can easily become extinct when better configurations of the software evolve. Take for example the extinction of VisiCalc by Lotus 1-2-3 and finally Microsoft Excel in the 1980s.
These three characteristics - component diversity, configurational exploration, and selection - which we conjecture represent conceptual equivalences for all evolving natural systems, may be sufficient to articulate a qualitative law-like statement that is not implicit in the classical laws of physics. In all instances, evolution is a process by which configurations with a greater degree of function are preferentially selected, while nonfunctional configurations are winnowed out. We conclude:
Systems of many interacting agents display an increase in diversity, distribution, and/or patterned behavior when numerous configurations of the system are subject to selective pressure.
However, is there a universal basis for selection? And is there a more quantitative formalism underlying this conjectured conceptual equivalence - a formalism rooted in the transfer of information? We elaborate on these questions here and argue that the answer to both questions is yes.
The authors then go on to propose their new physical law:
The Law of Increasing Functional Information:
The Functional Information of a system will increase (i.e., the system will evolve) if many different configurations of the system are subjected to selection for one or more functions.
In their view, all evolving systems can be seen to be conceptually equivalent in terms of a universal driving force of increasing Functional Information in action by means of a Law of Increasing Functional Information. In many previous softwarephysics posts, I have covered the pivotal role that self-replicating information has played in the history of our Universe and also in the evolution of software. For more on that see A Brief History of Self-Replicating Information. But under the more generalized Law of Increasing Functional Information, self-replicating information becomes just a subcategory of the grander concept of Functional Information.
Figure 2 – Imagine a pile of DNA, RNA or protein molecules of all possible sequences, sorted by activity with the most active at the top. A horizontal plane through the pile indicates a given level of activity; as this rises, fewer sequences remain above it. The Functional Information required to specify that activity is -log2 of the fraction of sequences above the plane. Expressing this fraction in terms of information provides a straightforward, quantitative measure of the difficulty of a task.
But what is Functional Information? Basically, Functional Information is information that can do things. It has agency. The concept of Functional Information was first introduced in a one-page paper:
Functional Information: Molecular messages
https://www.nature.com/articles/423689a
and is basically the use of Leon Brillouin's 1953 concept of information being a form of negative entropy that he abbreviated as "negentropy", but with a slight twist. The above paper introduces the concept of Functional Information as:
By analogy with classical information, Functional Information is simply -log2 of the probability that a random sequence will encode a molecule with greater than any given degree of function. For RNA sequences of length n, that fraction could vary from 4-n if only a single sequence is active, to 1 if all sequences are active. The corresponding functional information content would vary from 2n (the amount needed to specify a given random RNA sequence) to 0 bits. As an example, the probability that a random RNA sequence of 70 nucleotides will bind ATP with
micromolar affinity has been experimentally determined to be about 10-11. This corresponds to a functional information content of about 37 bits, compared with 140 bits to specify a unique 70-mer sequence. If there are multiple sequences with a given activity, then the corresponding Functional Information will always be less than the amount of information required to specify any particular sequence. It is important to note that Functional Information is not a property of any one molecule, but of the ensemble of all possible sequences, ranked by activity.
Imagine a pile of DNA, RNA or protein molecules of all possible sequences, sorted by activity with the most active at the top. A horizontal plane through the pile indicates a given level of activity; as this rises, fewer sequences remain above it. The Functional Information required to specify that activity is -log2 of the fraction of sequences above the plane. Expressing this fraction in terms of information provides a straightforward, quantitative measure of the difficulty of a task. More information is required to specify molecules that carry out difficult tasks, such as high-affinity binding or the rapid catalysis of chemical reactions with high energy barriers, than is needed to specify weak binders or slow catalysts. But precisely how much more Functional Information is required to specify a given increase in activity is unknown. If the mechanisms involved in improving activity are similar over a wide range of activities, then power-law behaviour might be expected. Alternatively, if it becomes progressively harder to improve activity as activity increases, then exponential behaviour may be seen. An interesting question is whether the relationship between Functional Information and activity will be similar in many different systems, suggesting that common principles are at work, or whether each case will be unique.
Indeed, any programmer could also imagine a similar pile of programs consisting of all possible sequences of source code with the buggiest versions at the bottom. When you reach the level of the intersecting plane, you finally reach those versions of source code that produce a program that actually provides the desired function. However, many of those programs that actually worked might be very inefficient or hard to maintain because of a sloppy coding style. As you move higher in the pile, the number of versions decreases but these versions produce the desired function more efficiently or are composed of cleaner code. As outlined above, the Functional Information required to specify such a software activity is -log2 of the fraction of source code programs above the plane.
The Softwarephysics of it All
Before going on to explain how the Law of Increasing Functional Information has affected the evolution of software over the past 2.6 billion seconds, let me tell you a bit about the origin of softwarephysics. I started programming in 1972 and finished up my B.S. in Physics at the University of Illinois at Urbana in 1973. I then headed up north to complete an M.S. in Geophysics at the University of Wisconsin at Madison. From 1975 – 1979, I was an exploration geophysicist exploring for oil, first with Shell, and then with Amoco. Then in 1979, I made a career change to become an IT professional. One very scary Monday morning, I was conducted to my new office cubicle in Amoco’s IT department, and I immediately found myself surrounded by a large number of very strange IT people, all scurrying about in a near state of panic, like the characters in Alice in Wonderland. Suddenly, it seemed like I was trapped in a frantic computer simulation, buried in punch card decks and fan-fold listings. After nearly 40 years in the IT departments of several major corporations, I can now state with confidence that most corporate IT departments can best be described as “frantic” in nature. This new IT job was a totally alien experience for me, and I immediately thought that I had just made a very dreadful mistake because I soon learned that being an IT professional was a lot harder than being an exploration geophysicist.
Figure 3 - As depicted back in 1962, George Jetson was a computer engineer in the year 2062, who had a full-time job working 3 hours a day, 3 days a week, pushing the same buttons that I pushed for 40 years as an IT professional.
But it was not supposed to be that way. As a teenager growing up in the 1960s, I was led to believe that in the 21st century, I would be leading the life of George Jetson, a computer engineer in the year 2062, who had a full-time job working 3 hours a day, 3 days a week, pushing buttons. But as a newly minted IT professional, I quickly learned that all you had to do was push the right buttons, in the right sequence, at the right time, and with zero errors. How hard could that be? Well, it turned out to be very difficult indeed!
To try to get myself out of this mess, I figured that if you could apply physics to geology; why not apply physics to software? So like the exploration team at Amoco that I had just left, consisting of geologists, geophysicists, paleontologists, geochemists, and petrophysicists, I decided to take all the physics, chemistry, biology, and geology that I could muster and throw it at the problem of software. The basic idea was that many concepts in physics, chemistry, biology, and geology suggested to me that the IT community had accidentally created a pretty decent computer simulation of the physical Universe on a grand scale, a Software Universe so to speak, and that I could use this fantastic simulation in reverse, to better understand the behavior of commercial software by comparing software to how things behaved in the physical Universe. Softwarephysics depicts software as a virtual substance and relies on our understanding of the current theories in physics, chemistry, biology, and geology to help us model the nature of software behavior. So in physics, we use software to simulate the behavior of the Universe, while in softwarephysics we use the Universe to simulate the behavior of software.
After a few months on the job, I began to suspect that the second law of thermodynamics was largely to blame from the perspective of statistical mechanics. I was always searching for the small population of programs that could perform a given function out of a nearly infinite population of programs that could not. It reminded me very much of Boltzmann's concept of entropy in statistical mechanics. The relatively few functional programs that I was searching for had a very low entropy relative to the vast population of buggy programs that did not. Worse yet, it seemed as though the second law of thermodynamics was constantly trying to destroy my programs whenever I did maintenance on them. That was because the second law was trying to insert new bugs into my programs whenever I changed my code. There were nearly an infinite number of ways to do it wrong and only a very few to do it right. But I am getting ahead of myself. To better understand all of this, please take note of the following thought experiment.
Figure 4 - We begin with a left compartment containing cold slow-moving nitrogen molecules (white circles) and a right compartment with hot fast-moving nitrogen molecules (black circles).
Figure 5 - Next, we perforate the divider between the compartments and allow the hot and cold nitrogen molecules to bounce off each other and exchange energies.
Figure 6 - After a period of time the two compartments will equilibrate to the same average temperature, but we will always find some nitrogen molecules bouncing around faster (black dots) and some nitrogen molecules bouncing around slower (white dots) than the average.
Recall that in 1738 Bernoulli proposed that gasses were really composed of a very large number of molecules bouncing around in all directions. Gas pressure in a cylinder was simply the result of a huge number of molecular impacts from individual gas molecules striking the walls of a cylinder, and heat was just a measure of the kinetic energy of the molecules bouncing around in the cylinder. In 1859, physicist James Clerk Maxwell took Bernoulli’s idea one step further. He combined Bernoulli’s idea of a gas being composed of a large number of molecules with the new mathematics of statistics. Maxwell reasoned that the molecules in a gas would not all have the same velocities. Instead, there would be a distribution of velocities; some molecules would move very quickly while others would move more slowly, with most molecules having a velocity around some average velocity. Now imagine that the two compartments in Figure 4 are filled with nitrogen gas, but that the left compartment is filled with cold slow-moving nitrogen molecules (white dots), while the right compartment is filled with hot fast-moving nitrogen molecules (black dots). If we perforate the partition between compartments, as in Figure 5 above, we will observe that the fast-moving hot molecules on the right will mix with and collide with the slow-moving cold molecules on the left and will give up kinetic energy to the slow-moving molecules. Eventually, both compartments will be found to be at the same temperature as shown in Figure 6, but we will always find some molecules moving faster than the average (black dots), and some molecules moving slower than the average (white dots) just as Maxwell had determined. This is called a state of thermal equilibrium and demonstrates a thermal entropy increase. We never observe a gas in thermal equilibrium suddenly dividing itself into hot and cold compartments all by itself. The gas can go from Figure 5 to Figure 6 but never the reverse because such a process would also be a violation of the second law of thermodynamics.
In 1867, Maxwell proposed a paradox along these lines known as Maxwell’s Demon. Imagine that we place a small demon at the opening between the two compartments and install a small trap door at this location. We instruct the demon to open the trap door whenever he sees a fast-moving molecule in the left compartment approach the opening to allow the fast-moving molecule to enter the right compartment. Similarly, when he sees a slow-moving molecule from the right compartment approach the opening, he opens the trap door to allow the low-temperature molecule to enter the left compartment. After some period of time, we will find that all of the fast-moving high-temperature molecules are in the right compartment and all of the slow-moving low-temperature molecules are in the left compartment. Thus the left compartment will become colder and the right compartment will become hotter in violation of the second law of thermodynamics (the gas would go from Figure 6 to Figure 5 above). With the aid of such a demon, we could run a heat engine between the two compartments to extract mechanical energy from the right compartment containing the hot gas as we dumped heat into the colder left compartment. This really bothered Maxwell, and he never found a satisfactory solution to his paradox. This paradox also did not help 19th-century physicists become more comfortable with the idea of atoms and molecules.
In 1929, Leo Szilárd became an instructor and researcher at the University of Berlin. There he published a paper, On the Decrease of Entropy in a Thermodynamic System by the Intervention of Intelligent Beings in 1929.
Figure 7 – In 1929 Szilard published a paper in which he explained that the process of the Demon knowing which side of a cylinder a molecule was in must produce some additional entropy to preserve the second law of thermodynamics.
In Szilárd's 1929 paper, he proposed that using Maxwell’s Demon, you could indeed build a 100% efficient steam engine in conflict with the second law of thermodynamics. Imagine a cylinder with just one water molecule bouncing around in it as in Figure 7(a). First, the Demon figures out if the water molecule is in the left half or the right half of the cylinder. If he sees the water molecule in the right half of the cylinder as in Figure 7(b), he quickly installs a piston connected to a weight via a cord and pulley. As the water molecule bounces off the piston in Figure 7(c) and moves the piston to the left, it slowly raises the weight and does some useful work on it. In the process of moving the piston to the left, the water molecule must lose kinetic energy in keeping with the first law of thermodynamics and slow down to a lower velocity and temperature than the atoms in the surrounding walls of the cylinder. When the piston has finally reached the far left end of the cylinder it is removed from the cylinder in preparation for the next cycle of the engine. The single water molecule then bounces around off the walls of the cylinder as in Figure 7(a), and in the process picks up additional kinetic energy from the jiggling atoms in the walls of the cylinder as they kick the water molecule back into the cylinder each time it bounces off the cylinder walls. Eventually, the single water molecule will once again be in thermal equilibrium with the jiggling atoms in the walls of the cylinder and will be on average traveling at the same velocity it originally had before it pushed the piston to the left. So this proposed engine takes the ambient high-entropy thermal energy of the cylinder’s surroundings and converts it into the useful low-entropy potential energy of a lifted weight. Notice that the first law of thermodynamics is preserved. The engine does not create energy; it simply converts the high-entropy thermal energy of the random motions of the atoms in the cylinder walls into useful low-entropy potential energy, but that does violate the second law of thermodynamics. Szilárd's solution to this paradox was simple. He proposed that the process of the Demon figuring out if the water molecule was in the left-hand side of the cylinder or the right-hand side of the cylinder must cause the entropy of the Universe to increase. So “knowing” which side of the cylinder the water molecule was in must come with a price; it must cause the entropy of the Universe to increase.
S = S0 - I A generalized second principle states that S must always increase. If an experiment yields an increase ΔI of the Information concerning a physical system, it must be paid for by a larger increase ΔS0 in the entropy of the system and its surrounding laboratory. The efficiency ε of the experiment is defined as ε = ΔI/ΔS0 ≤ 1. Moreover, there is a lower limit k ln2 (k, Boltzmann's constant) for the ΔS0 required in an observation. Some specific examples are discussed: length or distance measurements, time measurements, observations under a microscope. In all cases it is found that higher accuracy always means lower efficiency. The Information ΔI increases as the logarithm of the accuracy, while ΔS0 goes up faster than the accuracy itself. Exceptional circumstances arise when extremely small distances (of the order of nuclear dimensions) have to be measured, in which case the efficiency drops to exceedingly low values. This stupendous increase in the cost of observation is a new factor that should probably be included in the quantum theory.
Finally, in 1953 Leon Brillouin published a paper with a thought experiment explaining that Maxwell’s Demon required some Information to tell if a molecule was moving slowly or quickly. Brillouin defined this Information as negentropy, or negative entropy, and found that Information about the velocities of the oncoming molecules could only be obtained by the demon by bouncing photons off the moving molecules. Bouncing photons off the molecules increased the total entropy of the entire system whenever the demon determined if a molecule was moving slowly or quickly. So Maxwell's Demon was really not a paradox after all since even the Demon could not violate the second law of thermodynamics. Leon Brillouin's 1953 paper is available for purchase at:
Brillouin, L. (1953) The Negentropy Principle of Information. Journal of Applied Physics, 24, 1152-1163
https://doi.org/10.1063/1.1721463
But for the frugal folk, here is the abstract for Leon Brillouin’s famous 1953 paper:
The Negentropy Principle of Information
Abstract
The statistical definition of Information is compared with Boltzmann's formula for entropy. The immediate result is that Information I corresponds to a negative term in the total entropy S of a system.
In the equation above, Brillouin proposed that Information was a negative form of entropy. When an experiment yields some Information about a system, the total amount of entropy in the Universe must increase. Information is then essentially the elimination of microstates that a system can be found to exist in. From the above analysis, a change in Information ΔI is then the difference between the initial and final entropies of a system after a determination about the system has been made.
ΔI = Si - Sf
Si = initial entropy
Sf = final entropy
using the definition of entropy from the statistical mechanics of Ludwig Boltzmann. So we need to back up in time a bit and take a look at that next.
Beginning in 1866, Ludwig Boltzmann began work to extend Maxwell’s statistical approach. Boltzmann’s goal was to be able to explain all the macroscopic thermodynamic properties of bulk matter in terms of the statistical analysis of microstates. Boltzmann proposed that the molecules in a gas occupied a very large number of possible energy states called microstates, and for any particular energy level of a gas, there were a huge number of possible microstates producing the same macroscopic energy. The probability that the gas was in any one particular microstate was assumed to be the same for all microstates. In 1872, Boltzmann was able to relate the thermodynamic concept of entropy to the number of these microstates with the formula:
S = k ln(N)
S = entropy
N = number of microstates
k = Boltzmann’s constant
These ideas laid the foundations of statistical mechanics and its explanation of thermodynamics in terms of the statistics of the interactions of many tiny things.
The Physics of Poker
Boltzmann’s logic might be a little hard to follow, so let’s use an example to provide some insight by delving into the physics of poker. For this example, we will bend the formal rules of poker a bit. In this version of poker, you are dealt 5 cards as usual. The normal rank of the poker hands still holds and is listed below. However, in this version of poker, all hands of a similar rank are considered to be equal. Thus a full house consisting of a Q-Q-Q-9-9 is considered to be equal to a full house consisting of a 6-6-6-2-2 and both hands beat any flush. We will think of the rank of a poker hand as a macrostate. For example, we might be dealt 5 cards, J-J-J-3-6, and end up with the macrostate of three of a kind. The particular J-J-J-3-6 that we hold, including the suit of each card, would be considered a microstate. Thus for any particular rank of hand or macrostate, such as three of a kind, we would find a number of microstates. For example, for the macrostate of three of a kind, there are 54,912 possible microstates or hands that constitute the macrostate of three of a kind.
Rank of Poker Hands
Royal Flush - A-K-Q-J-10 all the same suit
Straight Flush - All five cards are of the same suit and in sequence
Four of a Kind - Such as 7-7-7-7
Full House - Three cards of one rank and two cards of another such as K-K-K-4-4
Flush - Five cards of the same suit, but not in sequence
Straight - Five cards in sequence, but not the same suit
Three of a Kind - Such as 5-5-5-7-3
Two Pair - Such as Q-Q-7-7-4
One Pair - Such as Q-Q-3-J-10
Next, we create a table using Boltzmann’s equation to calculate the entropy of each hand. For this example, we set Boltzmann’s constant k = 1, since k is just a “fudge factor” used to get the units of entropy using Boltzmann’s equation to come out to those used by the thermodynamic formulas of entropy.
Thus for three of a kind where N = 54,912 possible microstates or hands:
S = ln(N)
S = ln(54,912) = 10.9134872
| Hand | Number of Microstates N | Probability | Entropy = LN(N) | Information Change = Initial Entropy - Final Entropy |
| Royal Flush | 4 | 1.54 x 10-06 | 1.3862944 | 13.3843291 |
| Straight Flush | 40 | 1.50 x 10-05 | 3.6888795 | 11.0817440 |
| Four of a Kind | 624 | 2.40 x 10-04 | 6.4361504 | 8.3344731 |
| Full House | 3,744 | 1.44 x 10-03 | 8.2279098 | 6.5427136 |
| Flush | 5,108 | 2.00 x 10-03 | 8.5385632 | 6.2320602 |
| Straight | 10,200 | 3.90x 10-03 | 9.2301430 | 5.5404805 |
| Three of a Kind | 54,912 | 2.11 x 10-02 | 10.9134872 | 3.8571363 |
| Two Pairs | 123,552 | 4.75 x 10-02 | 11.7244174 | 3.0462061 |
| Pair | 1,098,240 | 4.23 x 10-01 | 13.9092195 | 0.8614040 |
| High Card | 1,302,540 | 5.01 x 10-01 | 14.0798268 | 0.6907967 |
| Total Hands | 2,598,964 | 1.00 | 14.7706235 | 0.0000000 |
Figure 8 – In the table above, each poker hand is a macrostate that has a number of microstates that all define the same macrostate. Given N, the number of microstates for each macrostate, we can then calculate its entropy using Boltzmann's definition of entropy S = ln(N) and its Information content using Leon Brillouin’s concept of Information ΔI = Si - Sf. The above table is available as an Excel spreadsheet on my Microsoft One Drive at Entropy .
Examine the above table. Note that higher-ranked hands have more order, less entropy, and are less probable than the lower-ranked hands. For example, a straight flush with all cards the same color, same suit, and in numerical order has an entropy = 3.6889, while a pair with two cards of the same value has an entropy = 13.909. A hand that is a straight flush appears more orderly than a hand that contains only a pair and is certainly less probable. A pair is more probable than a straight flush because more microstates produce the macrostate of a pair (1,098,240) than there are microstates that produce the macrostate of a straight flush (40). In general, probable things have lots of entropy and disorder, while improbable things, like perfectly bug-free software, have little entropy or disorder. In thermodynamics, entropy is a measure of the depreciation of a macroscopic system like how well mixed two gases are, while in statistical mechanics entropy is a measure of the microscopic disorder of a system, like the microscopic mixing of gas molecules. A pure container of oxygen gas will mix with a pure container of nitrogen gas because there are more arrangements or microstates for the mixture of the oxygen and nitrogen molecules than there are arrangements or microstates for one container of pure oxygen and the other of pure nitrogen molecules. In statistical mechanics, a neat room tends to degenerate into a messy room and increase in entropy because there are more ways to mess up a room than there are ways to tidy it up. In statistical mechanics, the second law of thermodynamics results because systems with lots of entropy and disorder are more probable than systems with little entropy or disorder, so entropy naturally tends to increase with time.
Getting back to Leon Brillouin’s concept of Information as a form of negative entropy, let’s compute the amount of Information you convey when you tell your opponent what hand you hold. When you tell your opponent that you have a straight flush, you eliminate more microstates than when you tell him that you have a pair, so telling him that you have a straight flush conveys more Information than telling him you hold a pair. For example, there are a total of 2,598,964 possible poker hands or microstates for a 5 card hand, but only 40 hands or microstates constitute the macrostate of a straight flush.
Strait Flush ΔI = Si – Sf = ln(2,598,964) – ln(40) = 11.082
For a pair we get:
Pair ΔI = Si – Sf = ln(2,598,964) – ln(1,098,240) = 0.8614040
When you tell your opponent that you have a straight flush you deliver 11.082 units of Information, while when you tell him that you have a pair you only deliver 0.8614040 units of Information. Clearly, when your opponent knows that you have a straight flush, he knows more about your hand than if you tell him that you have a pair.
Comparing Leon Brillouin’s Concept of Information to the Concept of Functional Information
From the above, we see that Leon Brillouin’s concept of Information dealt with determining how rare the results of a particular measurement were by determining how far the measurement was from the normal situation. This would essentially be the height of the intersecting plane in Figure 2. On the other hand, Functional Information is a measurement of the volume of the cone above the intersecting plane in Figure 2.
But before doing so, let's do a few mathematical operations on the definition of Functional Information. Recall that the concept of Functional Information is defined as the fraction of RNA strands or programs that can perform a given function. It is the fraction of things above the intersecting plane in Figure 2:
Functional Information = - log2( Na / (Nt )
where Na = number of RNA strands or programs above the intersecting plane of Figure 2
where Nt = total number of RNA strands or programs in Figure 2
Now using the magic of logarithms:
Functional Information = - log2 ( Na / Nt ) = - ( log2 ( Na) - log2 ( Nt ) ) = log2 ( Nt ) - log2 ( Na )
Now there really is nothing special about using the natural base-e logarithm ln(x) or the base-2 logarithm log2(x). Today, people sometimes like to use the base-2 logarithm log2(x) because we have computers that use base-2 arithmetic. But Boltzmann did not have a computer back in the 19th century so he used the common base-e natural logarithm ln(x) of the day. The mathematical constant e was first discovered in 1683 by Jacob Bernoulli while he was studying compound interest. He wondered what would happen if interest was compounded continuously, meaning an infinite number of times per year. The limit of this process led to the value of e, approximately 2.71828.
Now since ln(x) = 0.6931471806 log2(x) we can rewrite the equation as:
Functional Information = 0.6931471806 ( ln ( Nt ) - ln ( Na )
Since the 0.6931471806 is just a fudge factor to convert log2(x) to ln(x) we can just set it to "1" to obtain:
Functional Information = ln ( Nt ) - ln ( Na )
Now we can see that Functional Information is very similar to Brillouin's Information for poker:
Brillouin Information = ln ( Ntotal hands ) - ln ( Nyour hand )
Functional Information essentially compares the number of poker hands that are equal to or greater than your particular poker hand relative to all other possible poker hands, while Brillouin Information just compares your particular poker hand to all possible poker hands. The good news is that Functional Information does not get tangled up with the ideas of entropy and information used by network people.
The Very Sordid History of Entropy and Information in the Information Theory Used by Telecommunications
Claude Shannon went to work at Bell Labs in 1941 where he worked on cryptography and secret communications for the war effort. Claude Shannon was a true genius and is credited as being the father of Information Theory. But Claude Shannon was really trying to be the father of digital Communication Theory. In 1948, Claude Shannon published a very famous paper that got it all started.
A Mathematical Theory of Communication
https://people.math.harvard.edu/~ctm/home/text/others/shannon/entropy/entropy.pdf
Here is the very first paragraph from that famous paper:
Introduction
The recent development of various methods of modulation such as PCM and PPM which exchange bandwidth for signal-to-noise ratio has intensified the interest in a general theory of communication. A basis for such a theory is contained in the important papers of Nyquist and Hartley on this subject. In the present paper, we will extend the theory to include a number of new factors, in particular the effect of noise in the channel, and the savings possible due to the statistical structure of the original message and due to the nature of the final destination of the Information. The fundamental problem of communication is that of reproducing at one point either exactly or approximately a message selected at another point. Frequently the messages have meaning; that is they refer to or are correlated according to some system with certain physical or conceptual entities. These semantic aspects of communication are irrelevant to the engineering problem. The significant aspect is that the actual message is one selected from a set of possible messages. The system must be designed to operate for each possible selection, not just the one which will actually be chosen since this is unknown at the time of design. If the number of messages in the set is finite then this number or any monotonic function of this number can be regarded as a measure of the Information produced when one message is chosen from the set, all choices being equally likely.
Figure 9 – Above is the very first figure in Claude Shannon's very famous 1948 paper A Mathematical Theory of Communication.
Notice that the title of the paper is A Mathematical Theory of Communication and the very first diagram in the paper describes the engineering problem he was trying to solve. Claude Shannon was trying to figure out a way to send digital messages containing electrical bursts of 1s and 0s over a noisy transmission line. As shown in the red text above, Claude Shannon did not care at all about the Information in the message. The message could be the Gettysburg Address or pure jibberish. It did not matter. What mattered was being able to manipulate the noisy message of 1s and 0s so that the received message exactly matched the transmitted message. You see, at the time, AT&T was essentially only transmitting analog telephone conversations. A little noise on an analog telephone line is just like listening to an old scratchy vinyl record. It might be a little bothersome, but still understandable. However, error correction is very important when transmitting digital messages consisting of binary 1s and 0s. For example, both of the messages down below are encoded with a total of 16 1s and 0s:
0000100000000000
1001110010100101
However, the first message consists mainly of 0s, so it seems that it should be easier to apply some kind of error detection and correction scheme to the first message, compared to the second message, because the 1s are so rare in the first message. Doing the same thing for the second message should be much harder because the second message is composed of eight 0s and eight 1s. For example, simply transmitting the 16-bit message 5 times over and over should easily do the trick for the first message. But for the second message, you might have to repeat the 16 bits 10 times to make sure you could figure out the 16 bits in the presence of noise that could sometimes flip a 1 to a 0. This led Shannon to conclude that the second message must contain more Information than the first message. He also concluded that the 1s in the first message must contain more Information than the 0s because the 1s were much less probable than the 0s, and consequently, the arrival of a 1 had much more significance than the arrival of a 0 in the message. Using this line of reasoning, Shannon proposed that if the probability of receiving a 0 in a message was p and the probability of receiving a 1 in a message was q, then the Information H in the arrival of a single 1 or 0 must not simply be one bit of Information. Instead, it must depend upon the probabilities p and q of the arriving 1s and 0s:
H(p) = - p log2p - q log2q
Since in this case the message is only composed of 1s and 0s, it follows that:
q = 1 - p
Figure 10 shows a plot of the Information H(p) of the arrival of a 1 or 0 as a function of p the probability of a 0 arriving in a message when the message is only composed of 1s and 0s:
Figure 10 - A plot of Shannon’s Information Entropy equation H(p) versus the probability p of finding a 0 in a message composed solely of 1s and 0s
Notice that the graph peaks to a value of 1.0 when p = 0.50 and has a value of zero when p = 0.0 or p = 1.0. Now if p = 0.50 that means that q = 0.50 too because:
q = 1 - p
Substituting p = 0.50 and q = 0.50 into the above equation yields the Information content of an arriving 0 or 1 in a message, and we find that it is equal to one full bit of Information:
H(0.50) = -(0.50) log2(0.50) - (0.50) log2(0.50) = -log2(0.50) = 1
And we see that value of H(0.50) on the graph in Figure 10 does indeed have a value of 1 bit.
Now suppose the arriving message consists only of 0s. In that case, p = 1.0 and q = 0.0, and the Information content of an incoming 0 or 1 is H(1.0) and calculates out to a value of 0.0 in our equation and also in the plot of H(p) in Figure 10. This simply states that a message consisting simply of arriving 0s contains no Information at all. Similarly, a message consisting only of 1s would have a p = 0.0 and a q = 1.0, and our equation and plot calculate a value of H(0.0) = 0.0 too, meaning that a message simply consisting of 1s conveys no Information at all as well. What we see here is that seemingly a “messy” message consisting of many 1s and 0s conveys lots of Information, while a “neat” message consisting solely of 1s or 0s conveys no Information at all. When the probability of receiving a 1 or 0 in a message is 0.50 – 0.50, each arriving bit contains one full bit of Information, but for any other mix of probabilities, like 0.80 – 0.20, each arriving bit contains less than a full bit of Information. From the graph in Figure 10, we see that when a message has a probability mix of 0.80 – 0.20 that each arriving 1 or 0 only contains about 0.72 bits of Information. The graph also shows that it does not matter whether the 1s or the 0s are the more numerous bits because the graph is symmetric about the point p = 0.50, so a 0.20 – 0.80 mix of 1s and 0s also only delivers 0.72 bits of Information for each arriving 1 or 0.
Claude Shannon went on to generalize his formula for H(p) to include cases where there were more than two symbols used to encode a message:
H(p) = - Σ p(x) log2 p(x)
The above formula says that if you use 2, 3, 4, 5 …. different symbols to encode Information, just add up the probability of each symbol multiplied by the log2 of the probability of each symbol in the message. For example, suppose we choose the symbols 00, 01, 10, and 11 to send messages and that the probability of sending a 1 or a 0 are both 0.50. That means the probability p for each symbol 00, 01, 10 and 11 is 0.25 because each symbol is equally likely. So how much Information does each of these two-digit symbols now contain? If we substitute the values into Shannon’s equation we get an answer of 2 full bits of Information:
H(0.25, 0.25, 0.25, 0.25) = - 0.25 log2(0.25) - 0.25 log2(0.25) - 0.25 log2(0.25) - 0.25 log2(0.25) =
- log2(0.25) = 2
which makes sense because each symbol is composed of two one-bit symbols. In general, if all the symbols we use are N bits long, they will then all contain N bits of Information each. For example, in biology genes are encoded in DNA using four bases A, C, T and G. A codon consists of 3 bases and each codon codes for a particular amino acid or is an end of file Stop codon. On average, prokaryotic bacterial genes code for about 400 amino acids using 1200 base pairs. If we assume that the probability distribution for all four bases, A, C, T and G are the same for all the bases in a gene, namely a probability of 0.25, then we can use our analysis above to conclude that each base contains 2 bits of Information because we are using 4 symbols to encode the Information. That means a 3-base codon contains 6 bits of Information and a protein consisting of 400 amino acids contains 2400 bits of Information or 300 bytes of Information in IT speak.
Entropy and Information Confusion Now here is where the confusion comes in about the nature of Information. The story goes that Claude Shannon was not quite sure what to call his formula for H(p). Then one day in 1949 he happened to visit the mathematician and early computer pioneer John von Neumann, and that is when Information and entropy got mixed together in communications theory:
”My greatest concern was what to call it. I thought of calling it ‘Information’, but the word was overly used, so I decided to call it ‘uncertainty’. When I discussed it with John von Neumann, he had a better idea. Von Neumann told me, ‘You should call it entropy, for two reasons. In the first place, your uncertainty function has been used in statistical mechanics under that name, so it already has a name. In the second place, and more important, nobody knows what entropy really is, so in a debate you will always have the advantage.”
Unfortunately, with that piece of advice, we ended up equating Information with entropy in communications theory.
So in Claude Shannon's Information Theory people calculate the entropy, or Information content of a message, by mathematically determining how much “surprise” there is in a message. For example, in Claude Shannon's Information Theory, if I transmit a binary message consisting only of 1s or only of 0s, I transmit no useful Information because the person on the receiving end only sees a string of 1s or a string of 0s, and there is no “surprise” in the message. For example, the messages “1111111111” or “0000000000” are both equally boring and predictable, with no real “surprise” or Information content at all. Consequently, the entropy, or Information content, of each bit in these messages is zero, and the total Information of all the transmitted bits in the messages is also zero because they are both totally predictable and contain no “surprise”. On the other hand, if I transmit a signal containing an equal number of 1s and 0s, there can be lots of “surprise” in the message because nobody can really tell in advance what the next bit will bring, and each bit in the message then has an entropy, or Information content, of one full bit of Information.
This concept of entropy and Information content is very useful for people who work with transmission networks and on error detection and correction algorithms for those networks, but it is not very useful for IT professionals. For example, suppose you had a 10-bit software configuration file and the only “correct” configuration for your particular installation consisted of 10 1s in a row like this “1111111111”. In Claude Shannon's Information Theory that configuration file contains no Information because it contains no “surprise”. However, in Leon Brillouin’s formulation of Information there would be a total of N = 210 possible microstates or configuration files for the 10-bit configuration file, and since the only “correct” version of the configuration file for your installation is “1111111111” there are only N = 1 microstates that meet that condition.
Using the formulas above we can now calculate the entropy of our single “correct” 10-bit configuration file and the entropy of all possible 10-bit configuration files:
Boltzman's Definition of Entropy
S = ln(N)
N = Number of microstates
Leon Brillouin’s Definition of Information
∆Information = Si - Sf
Si = initial entropy
Sf = final entropy
as:
Sf = ln(1) = 0
Si = ln(210) = ln (1024) = 6.93147
So using Leon Brillouin’s formulation for the concept of Information the Information content of a single “correct” 10-bit configuration file is:
Si - Sf = 6.93147 – 0 = 6.93147
which, if you look at the table in Figure 8, contains a little more Information than drawing a full house in poker without drawing any additional cards and would be even less likely for you to stumble upon by accident than drawing a full house.
So in Claude Shannon's Information Theory, a very “buggy” 10 MB executable program file would contain just as much Information and would require just as many network resources to transmit as transmitting a bug-free 10 MB executable program file. Clearly, Claude Shannon's Information Theory formulations for the concepts of Information and entropy are less useful for IT professionals than are Leon Brillouin’s formulations for the concepts of Information and entropy.
What John von Neumann was trying to tell Claude Shannon was that his formula for H(p) looked very much like Boltzmann’s equation for entropy:
S = k ln(N)
The main difference was that Shannon was using a base 2 logarithm, log2 in his formula, while Boltzmann used a base e natural logarithm ln or loge in his formula for entropy. But given the nature of logarithms, that really does not matter much.
The main point of confusion arises because in communications theory the concepts of Information and entropy pertain to encoding and transmitting Information, while in IT and many other disciplines, like biology, we are more interested in the amounts of useful and useless Information in a message. For example, in communications theory, the code for a buggy 300,000-byte program contains just as much Information as a totally bug-free 300,000-byte version of the same program and would take just as much bandwidth and network resources to transmit accurately over a noisy channel as transmitting the bug-free version of the program. Similarly, in communications theory, a poker hand consisting of four Aces and a 2 of clubs contains just as much Information and is just as “valuable” as any other 5-card poker hand because the odds of being dealt any particular card is 1/52 for all the cards in a deck, and therefore, all messages consisting of 5 cards contain exactly the same amount of Information. Similarly, all genes that code for a protein consisting of 400 amino acids all contain exactly the same amount of Information, no matter what those proteins might be capable of doing. However, in both biology and IT we know that just one incorrect amino acid in a protein or one incorrect character in a line of code can have disastrous effects, so in those disciplines, the quantity of useful Information is much more important than the number of bits of data to be transmitted accurately over a communications channel.
Of course, the concepts of useful and useless Information lie in the eye of the beholder to some extent. Brillouin’s formula attempts to quantify this difference, but his formula relies upon Boltzmann’s equation for entropy, and Boltzmann’s equation has always had the problem of how do you define a macrostate? There really is no absolute way of defining one. For example, suppose I invented a new version of poker in which I defined the highest ranking hand to be an Ace of spades, 2 of clubs, 7 of hearts, 10 of diamonds and an 8 of spades. The odds of being dealt such a hand are 1 in 2,598,964 because there are 2,598,964 possible poker hands, and using Boltzmann’s equation that hand would have a very low entropy of exactly 0.0 because N = 1 and ln(1) = 0.0. Necessarily, the definition of a macrostate has to be rather arbitrary and tailored to the problem at hand. But in both biology and IT we can easily differentiate between macrostates that work as opposed to macrostates that do not work, like comparing a faulty protein or a buggy program with a functional protein or program.
My hope is that by now I have totally confused you about the true nature of entropy and Information with my explanations of both! If I have been truly successful, it now means that you have joined the intellectual elite who worry about such things. For most people
Information = Something you know
and that says it all.
For more on the above see Entropy - the Bane of Programmers, The Demon of Software, Some More Information About Information and The Application of the Second Law of Information Dynamics to Software and Bioinformatics.
Like Most Complex Systems - Software Displays Nonlinear Behavior
With a firm understanding of how Information behaves in our Universe, my next challenge as a softwarephysicist was to try to explain why the stack of software in Figure 2 was shaped like a cone. Why did the Universe demand near perfection in order for software to work? Why didn't the Universe at least offer some partial credit on my programs as my old physics professors did in college? When I made a little typo on a final exam, my professors usually did not tear up the whole exam and then give me an "F" for the entire course. But as a budding IT professional, I soon learned that computer compilers were not so kind. If I had one little typo in 100,000 lines of code, the compiler would happily abend my entire compile! Worse yet, when I did get my software to finally compile and link into an executable file that a computer could run, I always found that my software contained all sorts of little bugs that made it not run properly. Usually, my software would immediately crash and burn, but sometimes it would seem to run just fine for many weeks in Production and then suddenly crash and burn later for no apparent reason. This led me to realize that software generally exhibited nonlinear behavior, but with careful testing (selection), software could be made to operate in a linear manner.
Linear systems are defined by linear differential equations that can be solved using calculus. Linear systems are generally well-behaved meaning that a slight change to a linear system produces a well-behaved response. Nonlinear systems are defined by nonlinear differential equations that cannot be solved using calculus. Nonlinear differential equations can only be solved numerically by computers. Nonlinear systems are generally not well-behaved. A small change to a nonlinear system can easily produce disastrous results. This is true of both software and carbon-based life running on DNA. The mutation of a single character in 100,000 lines of code can easily produce disastrous results and so too can the mutation of a single base pair in the three billion base pairs that define a human being. The Law of Increasing Functional Information explains that evolving systems overcome this problem by generating large numbers of similar configurations that are later honed by selection processes that remove defective configurations.
Now it turns out that all of the fundamental classical laws of physics listed above are defined by linear differential equations. So you would think that this should not be a problem. And before we had computers that could solve nonlinear differential equations that is what everybody thought. But then in the 1950s, we started building computers that could solve nonlinear differential equations and that is when the trouble started. We slowly learned that nonlinear systems did not behave at all like their well-behaved cousins. With the aid of computer simulations, we learned that when large numbers of components were assembled, they began to follow nonlinear differential equations and exhibited nonlinear behaviors. True, each little component in the assemblage would faithfully follow the linear differential equations of the fundamental classical laws of physics, but when large numbers of components came together and began to interact, those linear differential equations went out the window. The result was the arrival of Chaos Theory in the 1970s. For more on that see Software Chaos.

Figure 11 – The orbit of the Earth about the Sun is an example of a linear system that is periodic and predictable. It is governed by the linear differential equations that define Newton's laws of motion and by his equation for the gravitational force.
Nonlinear systems are deterministic, meaning that once you set them off in a particular direction they always follow exactly the same path or trajectory, but they are not predictable because slight changes to initial conditions or slight perturbations can cause nonlinear systems to dramatically diverge to a new trajectory that leads to a completely different destination. Even when nonlinear systems are left to themselves and not perturbed in any way, they can appear to spontaneously jump from one type of behavior to another.
Figure 12 – Above is a very famous plot of the solution to three nonlinear differential equations developed by Ed Lorenz. Notice that like the orbit of the Earth about the Sun, points on the solution curve follow somewhat periodic paths about two strange attractors. Each attractor is called an attractor basin because points orbit the attractor basins like marbles in a bowl.
Figure 13 – But unlike the Earth orbiting the Sun, points in the attractor basins can suddenly jump from one attractor basin to another. High-volume corporate websites normally operate in a normal operations attractor basin but sometimes can spontaneously jump to an outage attractor basin even when they are only perturbed by a small processing load disturbance.
Figure 14 – The top-heavy SUVs of yore also had two basins of attraction and one of them was upside down.
For more on the above see Software Chaos.
The Fundamental Problem of Software
From the above analysis, I came to the realization in the early 1980s that my fundamental problem was that the second law of thermodynamics was constantly trying to destroy the useful information in my programs with small bugs, and because our Universe is largely nonlinear in nature, these small bugs could produce disastrous results when software was in Production. Now I would say that the second law of thermodynamics was constantly trying to destroy the Functional Information in my programs.
But the idea of destroying information causes some real problems for physicists, and as we shall see, the solution to that problem is that we need to make a distinction between useful information and useless information. Here is the problem that physicists have with destroying information. Recall, that a reversible process is a process that can be run backwards in time to return the Universe back to the state that it had before the process even began as if the process had never even happened in the first place. For example, the collision between two molecules at low energy is a reversible process that can be run backwards in time to return the Universe to its original state because Newton’s laws of motion are reversible. Knowing the position of each molecule at any given time and also its momentum, a combination of its speed, direction, and mass, we can predict where each molecule will go after a collision between the two, and also where each molecule came from before the collision using Newton’s laws of motion. For a reversible process such as this, the information required to return a system back to its initial state cannot be destroyed, no matter how many collisions might occur, in order for it to be classified as a reversible process that is operating under reversible physical laws.

Figure 15 – The collision between two molecules at low energy is a reversible process because Newton’s laws of motion are reversible (click to enlarge)
Currently, all of the effective theories of physics, what many people mistakenly now call the “laws” of the Universe, are indeed reversible, except for the second law of thermodynamics, but that is because, as we saw above, the second law is really not a fundamental “law” of the Universe at all. The second law of thermodynamics just emerges from the statistics of a large number of interacting particles. Now in order for a law of the Universe to be reversible, it must conserve information. That means that two different initial microstates cannot evolve into the same microstate at a later time. For example, in the collision between the blue and pink molecules in Figure 15, the blue and pink molecules both begin with some particular position and momentum one second before the collision and end up with different positions and momenta at one second after the collision. In order for the process to be reversible and Newton’s laws of motion to be reversible too, this has to be unique. A different set of identical blue and pink molecules starting out with different positions and momenta one second before the collision could not end up with the same positions and momenta one second after the collision as the first set of blue and pink molecules. If that were to happen, then one second after the collision, we would not be able to tell what the original positions and momenta of the two molecules were one second before the collision since there would now be two possible alternatives, and we would not be able to uniquely reverse the collision. We would not know which set of positions and momenta the blue and pink molecules originally had one second before the collision, and the information required to reverse the collision would be destroyed. And because all of the current effective theories of physics are time reversible in nature that means that information cannot be destroyed. So if someday information were indeed found to be destroyed in an experiment, the very foundations of physics would collapse, and consequently, all of science would collapse as well.
So if information cannot be destroyed, but Leon Brillouin’s reformulation of the second law of thermodynamics does imply that the total amount of information in the Universe must decrease (dS/dt > 0 implies that dI/dt < 0), what is going on? The solution to this problem is that we need to make a distinction between useful information and useless information. Recall that the first law of thermodynamics maintains that energy, like information, also cannot be created nor destroyed by any process. Energy can only be converted from one form of energy into another form of energy by any process. For example, when you drive to work, you convert all of the low entropy chemical energy in gasoline into an equal amount of useless waste heat energy by the time you hit the parking lot of your place of employment, but during the entire process of driving to work, none of the energy in the gasoline is destroyed, it is only converted into an equal amount of waste heat that simply diffuses away into the environment as your car cools down to be in thermal equilibrium with the environment. So why cannot I simply drive home later in the day using the ambient energy found around my parking spot? The reason you cannot do that is that pesky old second law of thermodynamics. You simply cannot turn the useless high-entropy waste heat of the molecules bouncing around near your parked car into useful low-entropy energy to power your car home at night. And the same goes for information. Indeed, the time reversibility of all the current effective theories of physics may maintain that you cannot destroy information, but that does not mean that you cannot change useful information into useless information.
But for all practical purposes from an IT perspective, turning useful information into useless information is essentially the same as destroying information. For example, suppose you take the source code file for a bug-free program and scramble its contents. Theoretically, the scrambling process does not destroy any information because theoretically it can be reversed. But in practical terms, you will be turning a low-entropy file into a useless high-entropy file that only contains useless information. So effectively you will have destroyed all of the useful information in the bug-free source code file. Here is another example. Suppose you are dealt a full house, K-K-K-4-4, but at the last moment a misdeal is declared and your K-K-K-4-4 gets shuffled back into the deck! Now the K-K-K-4-4 still exists as scrambled hidden information in the entropy of the entire deck, and so long as the shuffling process can be reversed, the K-K-K-4-4 can be recovered, and no information is lost, but that does not do much for your winnings. Since all the current laws of physics are reversible, including quantum mechanics, we should never see information being destroyed. In other words, because entropy must always increase and never decreases, the hidden information of entropy cannot be destroyed.
The Solution to the Fundamental Problem of Software
Again, in physics, we use software to simulate the behavior of the Universe, while in softwarephysics we use the Universe to simulate the behavior of software. So in the early 1980s, I asked myself, "Are there any very complicated systems in our Universe that seem to deal well with the second law of thermodynamics and nonlinearity?". I knew that living things did a great job with handling both, but at first, I did not know how to harness the power of living things to grow software instead of writing software. Then through a serendipitous accident, I began to do so by working on some software that I later called the Bionic Systems Development Environment (BSDE) back in 1985. BSDE was an early IDE (Integrated Development Environment) that ran on VM/CMS and grew applications from embryos in a biological manner. For more on BSDE see the last part of Programming Biology in the Biological Computation Group of Microsoft Research. During the 1980s, BSDE was used by about 30 programmers to put several million lines of code into Production. Here is a 1989 document on my Microsoft One Drive that was used by the IT Training department of Amoco in their BSDE class:
BSDE – A 1989 document describing how to use BSDE - the Bionic Systems Development Environment - to grow applications from genes and embryos within the maternal BSDE software.
Could the Physical Laws of our Universe Have also Arisen From the Law of Increasing Functional Information in Action?
Before embarking on the rather lengthy section below on the evolution of computer software and hardware, I would like to put in a plug for Lee Smolin's cosmological natural selection hypothesis that proposes that the physical laws of our Universe evolved from an infinitely long chain of previous Universes to produce a Universe that is complex enough to easily form black holes. In Lee Smolin's cosmological natural selection hypothesis, black holes in one universe produce white holes in new Universes beyond the event horizons of the originating black holes. These new Universes experience these new white holes as their own Big Bangs and then go on to produce their own black holes if possible. Thus, Universes that have physical laws that are good at making black holes are naturally selected for over Universes that do not and soon come to dominate the Multiverse. Lee Smolin's cosmological natural selection hypothesis meets all of the necessary requirements of the Law of Increasing Functional Information for the cosmic evolution of a Multiverse. For more on that see The Self-Organizing Recursive Cosmos.
The Evolution of Software as a Case Study of the Law of Increasing Functional Information in Action
In this rather long-winded tale, try to keep in mind the three required factors that the Law of Increasing Functional Information needs for a system to evolve:
1. Each system is formed from numerous interacting units (e.g., nuclear particles, chemical elements, organic molecules, or cells) that result in combinatorially large numbers of possible configurations.
2. In each of these systems, ongoing processes generate large numbers of different configurations.
3. Some configurations, by virtue of their stability or other “competitive” advantage, are more likely to persist owing to selection for function.
Also, take note of the coevolution of computer hardware and software. It is very similar to the coevolution of the rocks and minerals of the Earth's crust and carbon-based life over the past 4.0 billion years. Please feel free to skim over the details that only IT old-timers may find interesting.
The evolution of software provides a valuable case study for the Law of Increasing Functional Information because software has been evolving about 100 million times faster than did carbon-based life on this planet. This has been going on for the past 82 years, or 2.6 billion seconds, ever since Konrad Zuse first cranked up his Z3 computer in May of 1941. For more on the computational adventures of Konrad Zuse please see So You Want To Be A Computer Scientist?. More importantly, all of this software evolution has occurred within a single human lifetime and is well documented. So during a typical 40-year IT career of 1.26 billion seconds, one should expect to see some great changes take place as software rapidly evolves. In fact, all IT professionals find that they have to constantly retrain themselves to remain economically viable in the profession in order to keep up with the frantic pace of software evolution. Job insecurity due to technical obsolescence has always added to the daily mayhem of life in IT, especially for those supporting "legacy" software for a corporation. So as an IT professional, not only will you gain an appreciation for geological Deep Time, but you will also live through Deep Time as you observe software rapidly evolving during your career. To sample what might yet come, let us take a look at how software and hardware have coevolved over the past 2.6 billion seconds.
SoftwarePaleontology
Since the very beginning, the architecture of software has evolved through the Darwinian processes of inheritance, innovation and natural selection and has followed a path very similar to the path followed by the carbon-based living things on the Earth. I believe this has been due to what evolutionary biologists call convergence. For example, the concept of the eye has independently evolved at least 40 different times in the past 600 million years, and there are many examples of “living fossils” showing the evolutionary path. For example, the camera-like structures of the human eye and the eye of an octopus are nearly identical, even though each structure evolved totally independent of the other.
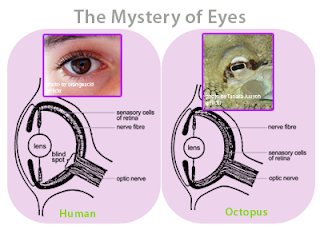
Figure 16 - The eye of a human and the eye of an octopus are nearly identical in structure, but evolved totally independently of each other. As Daniel Dennett pointed out, there are only a certain number of Good Tricks in Design Space and natural selection will drive different lines of descent towards them.
Figure 17 – There are many living fossils that have left behind signposts along the trail to the modern camera-like eye. Notice that the human-like eye on the far right is really that of an octopus (click to enlarge).
An excellent treatment of the significance that convergence has played in the evolutionary history of life on Earth, and possibly beyond, can be found in Life’s Solution (2003) by Simon Conway Morris. The convergent evolution for carbon-based life on the Earth to develop eyes was driven by the hardware fact of life that the Earth is awash in solar photons.
Programmers and living things both have to deal with the second law of thermodynamics and nonlinearity, and there are only a few optimal solutions. Programmers try new development techniques, and the successful techniques tend to survive and spread throughout the IT community, while the less successful techniques are slowly discarded. Over time, the population distribution of software techniques changes. As with the evolution of living things on Earth, the evolution of software has been greatly affected by the physical environment, or hardware, upon which it ran. Just as the Earth has not always been as it is today, the same goes for computing hardware. The evolution of software has been primarily affected by two things - CPU speed and memory size. As I mentioned in So You Want To Be A Computer Scientist?, the speed and memory size of computers have both increased by about a factor of a billion since Konrad Zuse built the Z3 in the spring of 1941, and the rapid advances in both and the dramatic drop in their costs have shaped the evolutionary history of software greatly.

Figure 18 - The Geological Time Scale of the Phanerozoic Eon is divided into the Paleozoic, Mesozoic and Cenozoic Eras by two great mass extinctions - click to enlarge.
Figure 19 - Life in the Paleozoic, before the Permian-Triassic mass extinction, was far different than life in the Mesozoic.
Figure 20 - In the Mesozoic the dinosaurs ruled after the Permian-Triassic mass extinction, but small mammals were also present.
Figure 21 - Life in the Cenozoic, following the Cretaceous-Tertiary mass extinction, has so far been dominated by the mammals. This will likely soon change as software becomes the dominant form of self-replicating information on the planet, ushering in a new geological Era that has yet to be named.
Currently, it is thought that these mass extinctions arise from two different sources. One type of mass extinction is caused by the impact of a large comet or asteroid and has become familiar to the general public as the Cretaceous-Tertiary (K-T) mass extinction that wiped out the dinosaurs at the Mesozoic-Cenozoic boundary 65 million years ago. An impacting mass extinction is characterized by a rapid extinction of species followed by a corresponding rapid recovery in a matter of a few million years. An impacting mass extinction is like turning off a light switch. Up until the day the impactor hits the Earth, everything is fine and the Earth has a rich biosphere. After the impactor hits the Earth, the light switch turns off and there is a dramatic loss of species diversity. However, the effects of the incoming comet or asteroid are geologically brief and the Earth’s environment returns to normal in a few decades or less, so within a few million years or so, new species rapidly evolve to replace those that were lost.
The other kind of mass extinction is thought to arise from an overabundance of greenhouse gases and a dramatic drop in oxygen levels and is typified by the Permian-Triassic (P-T) mass extinction at the Paleozoic-Mesozoic boundary 250 million years ago. Greenhouse extinctions are thought to be caused by periodic flood basalts, like the Siberian Traps flood basalt of the late Permian. A flood basalt begins as a huge plume of magma several hundred miles below the surface of the Earth. The plume slowly rises and eventually breaks the surface of the Earth, forming a huge flood basalt that spills basaltic lava over an area of millions of square miles to a depth of several thousand feet. Huge quantities of carbon dioxide bubble out of the magma over a period of several hundreds of thousands of years and greatly increase the ability of the Earth’s atmosphere to trap heat from the Sun. For example, during the Permian-Triassic mass extinction, carbon dioxide levels may have reached a level as high as 3,000 ppm, much higher than the current 420 ppm. Most of the Earth warms to tropical levels with little temperature difference between the equator and the poles. This shuts down the thermohaline conveyor that drives the ocean currents.
The Evolution of Software Over the Past 2.6 Billion Seconds Has Also Been Heavily Influenced by Mass Extinctions
Similarly, IT experienced a similar devastating mass extinction during the early 1990s when we experienced an environmental change that took us from the Age of the Mainframes to the Distributed Computing Platform. Suddenly mainframe Cobol/CICS and Cobol/DB2 programmers were no longer in demand. Instead, everybody wanted C and C++ programmers who worked on cheap Unix servers. This was a very traumatic time for IT professionals. Of course, the mainframe programmers never went entirely extinct, but their numbers were greatly reduced. The number of IT workers in mainframe Operations also dramatically decreased, while at the same time the demand for Operations people familiar with the Unix-based software of the new Distributed Computing Platform skyrocketed. This was around 1992, and at the time I was a mainframe programmer used to working with IBM's MVS and VM/CMS operating systems, writing Cobol, PL-1 and REXX code using DB2 databases. So I had to teach myself Unix and C and C++ to survive. In order to do that, I bought my very first PC, an 80-386 machine running Windows 3.0 with 5 MB of memory and a 100 MB hard disk for $1500. I also bought the Microsoft C7 C/C++ compiler for something like $300. And that was in 1992 dollars! One reason for the added expense was that there were no Internet downloads in those days because there were no high-speed ISPs. PCs did not have CD/DVD drives either, so the software came on 33 diskettes, each with a 1.44 MB capacity, that had to be loaded one diskette at a time in sequence. The software also came with about a foot of manuals describing the C++ class library on very thin paper. Indeed, suddenly finding yourself to be obsolete is not a pleasant thing and calls for drastic action. 
Figure 22 – An IBM OS/360 mainframe from 1964. The IBM OS/360 mainframe caused commercial software to explode within corporations and gave IT professionals the hardware platform that they were waiting for.
Figure 23 – The Distributed Computing Platform replaced a great deal of mainframe computing with a large number of cheap self-contained servers running software that tied the servers together.
The problem with the Distributed Computing Platform was that although the server hardware was cheaper than mainframe hardware, the granular nature of the Distributed Computing Platform meant that it created a very labor-intensive infrastructure that was difficult to operate and support, and as the level of Internet traffic dramatically expanded over the past 20 years, the Distributed Computing Platform became nearly impossible to support. For example, I worked in Middleware Operations for the Discover credit card company from 2002 - 2016, and during that time our Distributed Computing Platform infrastructure exploded by a factor of at least a hundred. It finally became so complex and convoluted that we could barely keep it all running, and we really did not even have enough change window time to properly apply maintenance to it as I described in The Limitations of Darwinian Systems. Clearly, the Distributed Computing Platform was not sustainable, and an alternative was desperately needed. This is because the Distributed Computing Platform was IT's first shot at running software on a multicellular architecture, as I described in Software Embryogenesis. But the Distributed Computing Platform simply had too many moving parts, all working together independently on their own, to fully embrace the advantages of a multicellular organization. In many ways, the Distributed Computing Platform was much like the ancient stromatolites that tried to reap the advantages of a multicellular organism by simply tying together the diverse interests of multiple layers of prokaryotic cyanobacteria into a "multicellular organism" that seemingly benefited the interests of all.
Figure 24 – Stromatolites are still found today in Sharks Bay Australia. They consist of mounds of alternating layers of prokaryotic bacteria.
Figure 25 – The cross-section of an ancient stromatolite displays the multiple layers of prokaryotic cyanobacteria that came together for their own mutual self-survival to form a primitive "multicellular" organism that seemingly benefited the interests of all. The servers and software of the Distributed Computing Platform were very much like the primitive stromatolites.
The collapse of the Distributed Computing Platform under its own weight brought on a second mass extinction beginning in 2010 with the rise of Cloud Computing.
The Rise of Cloud Computing Causes the Second Great Software Mass Extinction
The successor architecture to the Distributed Computing Platform was the Cloud Computing Platform, which is usually displayed as a series of services all stacked into levels. The highest level, SaaS (Software as a Service) runs the common third-party office software like Microsoft Office 365 and email. The second level, PaaS (Platform as a Service) is where the custom business software resides, and the lowest level, IaaS (Infrastructure as a Service) provides for an abstract tier of virtual servers and other resources that automatically scale with varying load levels. From an Applications Development standpoint, the PaaS layer is the most interesting because that is where they will be installing the custom application software used to run the business and also to run high-volume corporate websites that their customers use. Currently, that custom application software is installed into the middleware that is running on the Unix servers of the Distributed Computing Platform. The PaaS level will be replacing the middleware software, such as the Apache webservers and the J2EE Application servers, like WebSphere, Weblogic and JBoss that currently do that. For Operations, the IaaS level, and to a large extent, the PaaS level too are of most interest because those levels will be replacing the middleware and other support software running on hundreds or thousands of individual self-contained servers. The Cloud architecture can be run on a company's own hardware, or it can be run on a timesharing basis on the hardware at Amazon, Microsoft, IBM or other Cloud providers, using the Cloud software that the Cloud providers market.
Figure 26 – Cloud Computing returns us to the timesharing days of the 1960s and 1970s by viewing everything as a service.
Basically, the Cloud Computing Platform is based on two defining characteristics:
1. Returning to the timesharing days of the 1960s and 1970s when many organizations could not afford to support a mainframe infrastructure of their own.
2. Taking the multicellular architecture of the Distributed Computing Platform to the next level by using Cloud Platform software to produce a full-blown multicellular organism, and even higher, by introducing the self-organizing behaviors of the social insects like ants and bees.
For more on this see Cloud Computing and the Coming Software Mass Extinction and The Origin and Evolution of Cloud Computing - Software Moves From the Sea to the Land and Back Again.
The Geological Time Scale of Software Evolution
Similarly, the evolutionary history of software over the past 2.6 billion seconds has also been greatly affected by a series of mass extinctions, which allow us to also subdivide the evolutionary history of software into several long computing eras, like the geological eras listed above. As with the evolution of the biosphere over the past 541 million years, we shall see that these mass extinctions of software have also been caused by several catastrophic events in IT that were separated by long periods of slow software evolution through uniformitarianism. Like the evolution of carbon-based life on the Earth, some of these software mass extinctions were caused by some drastic environmental hardware changes, while others were simply caused by drastic changes in the philosophy of software development thought.
Unstructured Period (1941 – 1972)
During the Unstructured Period, programs were simple monolithic structures with lots of GOTO statements, no subroutines, no indentation of code, and very few comment statements. The machine code programs of the 1940s evolved into the assembler programs of the 1950s and the compiled programs of the 1960s, with FORTRAN appearing in 1956 and COBOL in 1958. These programs were very similar to the early prokaryotic bacteria that appeared over 4,000 million years ago on Earth and lacked internal structure. Bacteria essentially consist of a tough outer cell wall enclosing an inner cell membrane and contain a minimum of internal structure. The cell wall is composed of a tough molecule called peptidoglycan, which is composed of tightly bound amino sugars and amino acids. The cell membrane is composed of phospholipids and proteins, which will be described later in this posting. The DNA within bacteria generally floats freely as a large loop of DNA, and their ribosomes, used to help transcribe DNA into proteins, float freely as well and are not attached to membranes called the rough endoplasmic reticulum. The chief advantage of bacteria is their simple design and ability to thrive and rapidly reproduce even in very challenging environments, like little AK-47s that still manage to work in environments where modern tanks fail. Just as bacteria still flourish today, some unstructured programs are still in production.

Figure 27 – A simple prokaryotic bacterium with little internal structure (click to enlarge)
Below is a code snippet from a fossil FORTRAN program listed in a book published in 1969 showing little internal structure. Notice the use of GOTO statements to skip around in the code. Later this would become known as the infamous “spaghetti code” of the Unstructured Period that was such a joy to support.
30 DO 50 I=1,NPTS
31 IF (MODE) 32, 37, 39
32 IF (Y(I)) 35, 37, 33
33 WEIGHT(I) = 1. / Y(I)
GO TO 41
35 WEIGHT(I) = 1. / (-1*Y(I))
37 WEIGHT(I) = 1.
GO TO 41
39 WEIGHT(I) = 1. / SIGMA(I)**2
41 SUM = SUM + WEIGHT(I)
YMEAN = WEIGHT(I) * FCTN(X, I, J, M)
DO 44 J = 1, NTERMS
44 XMEAN(J) = XMEAN(J) + WEIGHT(I) * FCTN(X, I, J, M)
50 CONTINUE
The primitive nature of software in the Unstructured Period was largely due to the primitive nature of the hardware upon which it ran. Figure 22 shows an IBM OS/360 from 1964 – notice the operator at the teletype feeding commands to the nearby operator console, the distant tape drives, and the punch card reader in the mid-ground. Such a machine had about 1 MB of memory, less than 1/8000 of the memory of a current cheap $250 PC, and a matching anemic processing speed. For non-IT readers let me remind all that:
1 KB = 1 kilobyte = 210 = 1024 bytes or about 1,000 bytes
1 MB = 1 megabyte = 1024 x 1024 = 1,048,576 bytes or about a million bytes
1 GB = 1 gigabyte = 1024 x 10224 x 1024 = 1,073,741,824 bytes or about a billion bytes
One byte of memory can store one ASCII text character like an “A” and two bytes can store a small integer in the range of -32,768 to +32,767. When I first started programming in 1972 we thought in terms of kilobytes, then megabytes, and now gigabytes. Data science people now think in terms of many terabytes - 1 TB = 1024 GB.
Software was input via punched cards and the output was printed on fan-fold paper. Compiled code could be stored on tape or very expensive disk drives if you could afford them, but any changes to code were always made via punched cards, and because you were only allowed perhaps 128K – 256K of memory for your job, programs had to be relatively small, so simple unstructured code ruled the day. Like the life cycle of a single-celled bacterium, the compiled and linked code for your program was loaded into the memory of the computer at execution time and did its thing in a batch mode, until it completed successfully or abended and died. At the end of the run, the computer’s memory was released for the next program to be run and your program ceased to exist.

Figure 28 - An IBM 029 keypunch machine from the 1960s Unstructured Period of software.

Figure 29 - Each card could hold a maximum of 80 bytes. Normally, one line of code was punched onto each card.

Figure 30 - The cards for a program were held together into a deck with a rubber band, or for very large programs, the deck was held in a special cardboard box that originally housed blank cards. Many times the data cards for a run followed the cards containing the source code for a program. The program was compiled and linked in two steps of the run and then the generated executable file processed the data cards that followed in the deck.

Figure 31 - To run a job, the cards in a deck were fed into a card reader, as shown on the left above, to be compiled, linked, and executed by a million-dollar mainframe computer. In the above figure, the mainframe is located directly behind the card reader.
Figure 32 - The output of programs was printed on fan-folded paper by a line printer.
However, one should not discount the great advances that were made by the early bacteria billions of years ago or by the unstructured code from the computer systems of the 1950s and 1960s. These were both very important formative periods in the evolution of life and of software on Earth, and examples of both can still be found in great quantities today. For example, it is estimated that about 50% of the Earth’s biomass is still composed of simple bacteria. Your body consists of about 100 trillion cells, but you also harbor about 10 times that number of bacterial cells that are in a parasitic/symbiotic relationship with the “other” cells of your body and perform many of the necessary biochemical functions required to keep you alive, such as aiding with the digestion of food. Your gut contains about 3.5 pounds of active bacteria and about 50% of the dry weight of your feces is bacteria, so in reality, we are all composed of about 90% bacteria with only 10% of our cells being “normal” human cells.
All of the fundamental biochemical pathways used by living things to create large complex organic molecules from smaller monomers, or to break those large organic molecules back down into simple monomers were first developed by bacteria billions of years ago. For example, bacteria were the first forms of life to develop the biochemical pathways that turn carbon dioxide, water, and the nitrogen in the air into the organic molecules necessary for life – sugars, lipids, amino acids, and the nucleotides that form RNA and DNA. They also developed the biochemical pathways to replicate DNA and transcribe DNA into proteins, and to form complex structures such as cell walls and cell membranes from sugars, amino acids, proteins, and phospholipids. Additionally, bacteria invented the Krebs cycle to break these large macromolecules back down to monomers for reuse and to release and store energy by transforming ADP to ATP. To expand upon this, we will see in Software Symbiogenesis, how Lynn Margulis has proposed that all the innovations of large macroscopic forms of life have actually been acquired from the highly productive experiments of bacterial life forms.
Similarly, all of the fundamental coding techniques of IT at the line of code level were first developed in the Unstructured Period of the 1950s and 1960s, such as the use of complex variable names, arrays, nested loops, loop counters, if-then-else logic, list processing with pointers, I/O blocking, bubble sorts, etc. When I was in Middleware Operations for Discover, I did not do much coding. However, I did write a large number of Unix shell scripts to help make my job easier. These Unix shell scripts were small unstructured programs in the range of 10 – 50 lines of code, and although they were quite primitive and easy to write, they had a huge economic pay-off for me. Many times, a simple 20 line Unix shell script that took less than an hour to write, would provide as much value to me as the code behind the IBM Websphere Console, which I imagine probably had cost IBM about $10 - $100 million dollars to develop and came to several hundred thousand lines of code. For more on that see MISE in the Attic. So if you add up all the little unstructured Unix shell scripts, DOS .bat files, edit macros, Excel spreadsheet macros, Word macros, etc., I bet that at least 50% of the software in the Software Universe is still unstructured code.
Figure 33 – An IBM OS/360 mainframe from 1964. The IBM OS/360 mainframe caused commercial software to explode within corporations during the Unstructured Period and gave IT professionals the hardware platform that they were waiting for.
Structured Period (1972 – 1992)
The increasing availability of computers with more memory and faster CPUs allowed for much larger programs to be written in the 1970s, but unstructured code became much harder to maintain as it grew in size, so the need for internal structure became readily apparent. Plus, around this time code began to be entered via terminals using full-screen editors, rather than on punched cards, which made it easier to view larger sections of code as you changed it.
Figure 34 - IBM 3278 terminals were connected to controllers that connected to IBM mainframes The IBM 3278 terminals then ran interactive TSO sessions with the IBM mainframes. The ISPF full-screen editor was then brought up under TSO after you logged into a TSO session.
Figure 35 – A mainframe with IBM 3278 CRT terminals attached (click to enlarge)
In 1972, Dahl, Dijkstra, and Hoare published Structured Programming, in which they suggested that computer programs should have complex internal structure with no GOTO statements, lots of subroutines, indented code, and many comment statements. During the Structured Period, these structured programming techniques were adopted by the IT community, and the GOTO statements were replaced by subroutines, also known as functions(), and indented code with lots of internal structure, like the eukaryotic structure of modern cells that appeared about 1,500 million years ago. Eukaryotic cells are found in the bodies of all complex organisms from single-cell yeasts to you and me and divide up cell functions amongst a collection of organelles (subroutines), such as mitochondria, chloroplasts, Golgi bodies, and the endoplasmic reticulum. 
Figure 36 – Plants and animals are composed of eukaryotic cells with much internal structure (click to enlarge)
Figure 37 compares the simple internal structure of a typical prokaryotic bacterium with the internal structure of eukaryotic plant and animal cells. These eukaryotic cells could be simple single-celled plants and animals or they could be found within a much larger multicellular organism consisting of trillions of eukaryotic cells. Figure 37 is a bit deceiving, in that eukaryotic cells are huge cells that are more than 20 times larger in diameter than a typical prokaryotic bacterium with about 10,000 times the volume as shown in Figure 38. Because eukaryotic cells are so large, they have an internal cytoskeleton, composed of linear-shaped proteins that form filaments that act like a collection of tent poles, to hold up the huge cell membrane encircling the cell.
Eukaryotic cells also have a great deal of internal structure, in the form of organelles, that are enclosed by internal cell membranes. Like the structured programs of the 1970s and 1980s, eukaryotic cells divide up functions amongst these organelles. These organelles include the nucleus to store and process the genes stored in DNA, mitochondria to perform the Krebs cycle to create ATP from carbohydrates, and chloroplasts in plants to produce energy-rich carbohydrates from water, carbon dioxide, and sunlight.
Figure 37 – The prokaryotic cell architecture of the bacteria and archaea is very simple and designed for rapid replication. Prokaryotic cells do not have a nucleus enclosing their DNA. Eukaryotic cells, on the other hand, store their DNA on chromosomes that are isolated in a cellular nucleus. Eukaryotic cells also have a very complex internal structure with a large number of organelles, or subroutine functions, that compartmentalize the functions of life within the eukaryotic cells.
Figure 38 – Not only are eukaryotic cells much more complicated than prokaryotic cells, but they are also HUGE!
The introduction of structured programming techniques in the early 1970s allowed programs to become much larger and much more complex by using many subroutines to divide up logic into self-contained organelles. This induced a mass extinction of unstructured programs, similar to the Permian-Triassic (P-T) mass extinction, or the Great Dying, 250 million years ago that divided the Paleozoic from the Mesozoic in the stratigraphic column and resulted in the extinction of about 90% of the species on Earth. As programmers began to write new code using the new structured programming paradigm, older code that was too difficult to rewrite in a structured manner remained as legacy “spaghetti code” that slowly fossilized over time in Production. Like the Permian-Triassic (P-T) mass extinction, the mass extinction of unstructured code in the 1970s was more like a greenhouse gas mass extinction than an impactor mass extinction because it spanned nearly an entire decade, and was also a rather complete mass extinction which totally wiped out most unstructured code in corporate systems.
Below is a code snippet from a fossil COBOL program listed in a book published in 1975. Notice the structured programming use of indented code and calls to subroutines with PERFORM statements.
PROCEDURE DIVISION.
OPEN INPUT FILE-1, FILE-2
PERFORM READ-FILE-1-RTN.
PERFORM READ-FILE-2-RTN.
PERFORM MATCH-CHECK UNTIL ACCT-NO OF REC-1 = HIGH_VALUES.
CLOSE FILE-1, FILE-2.
MATCH-CHECK.
IF ACCT-NO OF REC-1 < ACCT-NO OF REC-2
PERFORM READ-FILE-1-RTN
ELSE
IF ACCT-NO OF REC-1 > ACCT-NO OF REC-2
DISPLAY REC-2, 'NO MATCHING ACCT-NO'
PERORM READ-FILE-1-RTN
ELSE
PERORM READ-FILE-2-RTN UNTIL ACCT-NO OF REC-1
NOT EQUAL TO ACCT-NO OF REC-2
When I encountered my very first structured FORTRAN program in 1975, I diligently “fixed” the program by removing all the code indentations! You see in those days, we rarely saw the entire program on a line printer listing because that took a compile of the program to produce and wasted valuable computer time, which was quite expensive back then. When I provided an estimate for a new system back then, I figured 25% for programming manpower, 25% for overhead charges from other IT groups on the project, and 50% for compiles. So instead of working with a listing of the program, we generally flipped through the card deck of the program to do debugging. Viewing indented code in a card deck can give you a real headache, so I just “fixed” the program by making sure all the code started in column 7 of the punch cards as it should!
Object-Oriented Period (1992 – Present)
During the Object-Oriented Period, programmers adopted a multicellular organization for software, in which programs consisted of many instances of objects (cells) that were surrounded by membranes studded with exposed methods (membrane receptors).
The following discussion might be a little hard to follow for readers with a biological background, but with little IT experience, so let me define a few key concepts with their biological equivalents.
Class – Think of a class as a cell type. For example, the class Customer is a class that defines the cell type of Customer and describes how to store and manipulate the data for a Customer, like firstName, lastName, address, and accountBalance. For example, a program might instantiate a Customer object called “steveJohnston”.
Object – Think of an object as a cell. A particular object will be an instance of a class. For example, the object steveJohnston might be an instance of the class Customer and will contain all the information about my particular account with a corporation. At any given time, there could be many millions of Customer objects bouncing around in the IT infrastructure of a major corporation’s website.
Instance – An instance is a particular object of a class. For example, the steveJohnston object would be a particular instance of the class Customer, just as a particular red blood cell would be a particular instance of the cell type RedBloodCell. Many times programmers will say things like “This instantiates the Customer class”, meaning it creates objects (cells) of the Customer class (cell type).
Method – Think of a method() as a biochemical pathway. It is a series of programming steps or “lines of code” that produce a macroscopic change in the state of an object (cell). The Class for each type of object defines the data for the class, like firstName, lastName, address, and accountBalance, but it also defines the methods() that operate upon these data elements. Some methods() are public, while others are private. A public method() is like a receptor on the cell membrane of an object (cell). Other objects(cells) can send a message to the public methods of an object (cell) to cause it to execute a biochemical pathway within the object (cell). For example, steveJohnston.setFirstName(“Steve”) would send a message to the steveJohnston object instance (cell) of the Customer class (cell type) to have it execute the setFirstName method() to change the firstName of the object to “Steve”. The steveJohnston.getaccountBalance() method would return my current account balance with the corporation. Objects also have many internal private methods() within that are biochemical pathways that are not exposed to the outside world. For example, the calculateAccountBalance() method could be an internal method that adds up all of my debits and credits and updates the accountBalance data element within the steveJohnston object, but this method cannot be called by other objects (cells) outside of the steveJohnston object (cell). External objects (cells) have to call the steveJohnston.getaccountBalance() in order to find out my accountBalance.
Line of Code – This is a single statement in a method() like:
discountedTotalCost = (totalHours * ratePerHour) - costOfNormalOffset;
Remember methods() are the equivalent of biochemical pathways and are composed of many lines of code, so each line of code is like a single step in a biochemical pathway. Similarly, each character in a line of code can be thought of as an atom, and each variable as an organic molecule. Each character can be in one of 256 ASCII quantum states defined by 8 quantized bits, with each bit in one of two quantum states “1” or “0”, which can also be characterized as 8 electrons in a spin-up ↑ or spin-down ↓ state:
discountedTotalCost = (totalHours * ratePerHour) - costOfNormalOffset;
C = 01000011 = ↓ ↑ ↓ ↓ ↓ ↓ ↑ ↑
H = 01001000 = ↓ ↑ ↓ ↓ ↑ ↓ ↓ ↓
N = 01001110 = ↓ ↑ ↓ ↓ ↑ ↑ ↑ ↓
O = 01001111 = ↓ ↑ ↓ ↓ ↑ ↑ ↑ ↑
Programmers have to assemble characters (atoms) into organic molecules (variables) to form the lines of code that define a method() (biochemical pathway). As in carbon-based biology, the slightest error in a method() can cause drastic and usually fatal consequences. Because there is nearly an infinite number of ways of writing code incorrectly and only a very few ways of writing code correctly, there is an equivalent of the second law of thermodynamics at work. This simulated second law of thermodynamics and the very nonlinear macroscopic effects that arise from small coding errors is why software architecture has converged upon Life’s Solution. With these concepts in place, we can now proceed with our comparison of the evolution of software and carbon-based life on Earth.
Object-oriented programming actually started in the 1960s with Simula, the first language to use the concept of merging data and functions into objects defined by classes, but object-oriented programming did not really catch on until nearly 30 years later:
1962 - 1965 Dahl and Nygaard develop the Simula language
1972 - Smalltalk language developed
1983 - 1985 Sroustrup develops C++
1995 - Sun announces Java at SunWorld `95
Similarly, multicellular organisms first appeared about 900 million years ago, but it took about another 400 million years, until the Cambrian, for it to catch on as well. Multicellular organisms consist of huge numbers of cells that send messages between cells (objects) by secreting organic molecules that bind to the membrane receptors on other cells and induce those cells to execute exposed methods. For example, your body consists of about 100 trillion independently acting eukaryotic cells, and not a single cell in the collection knows that the other cells even exist. In an object-oriented manner, each cell just responds to the organic molecules that bind to its membrane receptors, and in turn, sends out its own set of chemical messages that bind to the membrane receptors of other cells in your body. When you wake to the sound of breaking glass in the middle of the night, your adrenal glands secrete the hormone adrenaline (epinephrine) into your bloodstream, which binds to the getScared() receptors on many of your cells. In an act of object-oriented polymorphism, your liver cells secrete glucose into your bloodstream, and your heart cells constrict harder when their getScared() methods are called.
Figure 39 – Multicellular organisms consist of a large number of eukaryotic cells, or objects, all working together (click to enlarge)
These object-oriented languages use the concepts of encapsulation, inheritance and polymorphism which is very similar to the multicellular architecture of large organisms
Encapsulation
Objects are contiguous locations in memory that are surrounded by a virtual membrane that cannot be penetrated by other code and are similar to an individual cell in a multicellular organism. The internal contents of an object can only be changed via exposed methods (like subroutines), similar to the receptors on the cellular membranes of a multicellular organism. Each object is an instance of an object class, just as individual cells are instances of a cell type. For example, an individual red blood cell is an instance object of the red blood cell class.
Inheritance
Cells inherit methods in a hierarchy of human cell types, just as objects form a class hierarchy of inherited methods in a class library. For example, all cells have the metabolizeSugar() method, but only red blood cells have the makeHemoglobin() method. Below is a tiny portion of the 210 known cell types of the human body arranged in a class hierarchy.
Human Cell Classes
1. Epithelium
2. Connective Tissue
A. Vascular Tissue
a. Blood
- Red Blood Cells
b. Lymph
B. Proper Connective Tissue
3. Muscle
4. Nerve
Polymorphism
A chemical message sent from one class of cell instances can produce an abstract behavior in other cells. For example, adrenal glands can send the getScared() message to all cell instances in your body, but all of the cell instances getScared() in their own fashion. Liver cells release glucose and heart cells contract faster when their getScared() methods are called. Similarly, when you call the print() method of a report object, you get a report, and when you call the print() method of a map, you get a map.
Figure 40 – Objects are like cells in a multicellular organism that exchange messages with each other (click to enlarge)
The object-oriented revolution, enhanced by the introduction of Java in 1995, caused another mass extinction within IT as structured procedural programs began to be replaced by object-oriented C++ and Java programs, like the Cretaceous-Tertiary extinction 65 million years ago that killed off the dinosaurs, presumably caused by a massive asteroid strike upon the Earth.
Below is a code snippet from a fossil C++ program listed in a book published in 1995. Notice the object-oriented programming technique of using a class specifier to define the data and methods() of objects instantiated from the class. Notice that PurchasedPart class inherits code from the more generic Part class. In both C++ and Java, variables and methods that are declared private can only be used by a given object instance, while public methods can be called by other objects to cause an object to perform a certain function, so public methods are very similar to the functions that the cells in a multicellular organism perform when organic molecules bind to the membrane receptors of their cells. Later in this posting, we will describe in detail how multicellular organisms use this object-oriented approach to isolate functions.
class PurchasedPart : public Part
private:
int partNumber;
char description[20]
public:
PurchasedPart(int pNum, char* desc);
PurchasePart();
void setPart(int pNum, char* desc);
char* getDescription();
void main()
PurchasedPart Nut(1, "Brass");
Nut.setPart(1, "Copper");
Figure 41 – Cells in a growing embryo communicate with each other by sending out ligand molecules called paracrine factors that bind to membrane receptors on other cells.
Figure 42 – Calling a public method of an Object can initiate the execution of a cascade of private internal methods within the Object. Similarly, when a paracrine factor molecule plugs into a receptor on the surface of a cell, it can initiate a cascade of internal biochemical pathways. In the above figure, an Ag protein plugs into a BCR receptor and initiates a cascade of biochemical pathways or methods within a cell.
Like the geological eras, the Object-Oriented Period got a kick-start from an environmental hardware change. In the early 1990s, the Distributed Computing Revolution hit with full force, which spread computing processing over a number of servers and client PCs, rather than relying solely on mainframes to do all the processing. It began in the 1980s with the introduction of PCs into the office to do stand-alone things like word processing and spreadsheets. The PCs were also connected to mainframes as dumb terminals through emulator software as shown in Figure 35 above. In this architectural topology, the mainframes still did all the work and the PCs just displayed CICS green screens like dumb terminals. But this at least eliminated the need to have an IBM 3278 terminal and PC on a person’s desk, which would have left very little room for anything else! But this architecture wasted all the computing power of the rapidly evolving PCs, so the next step was to split the processing load between the PCs and a server. This was known as the 2-tier client/server or “thick client” architecture of Figure 43. In 2-tier client/server, the client PCs ran the software that displayed information in a GUI like Windows 3.0 and connected to a server running RDBMS (Relational Database Management System) software like Oracle or Sybase that stored the common data used by all the client PCs. This worked great so long as the number of PCs remained under about 30. We tried this at Amoco in the early 1990s, and it was like painting the Eiffel Tower. As soon as we got the 30th PC working, we had to go back and fix the first one! It was just too hard to keep the “thick client” software up and running on all those PCs with all the other software running on them that varied from machine to machine.
These problems were further complicated by the rise of computer viruses in the mid-1980s. Prior to the 2-tier client/server architecture, many office PCs were standalone machines, only connected to mainframes as dumb terminals, and thus totally isolated machines safe from computer virus infection. In the PC topology of the 1980s, computer viruses could only spread via floppy disks, which severely limited their infection rates. But once the 2-tier architecture fell into place, office PCs began to be connected together via LANs (Local Area Networks) and WANs (Wide Area Networks) to share data and other resources like printers. This provided a very friendly environment for computer viruses to quickly spread across an entire enterprise, so the other thing that office PCs began to share was computer viruses. Computer viruses are purely parasitic forms of software, which are more fully covered in postings on Self-Replicating Information and Software Symbiogenesis.
The limitations of the 2-tier architecture led to the 3-tier model in the mid to late 1990s with the advent of “middleware” as seen in Figure 43. Middleware is software that runs on servers between the RDBMS servers and the client PCs. In the 3-tier architecture, the client PCs run “thin client” software that primarily displays information via a GUI like Windows. The middleware handles all the business logic and relies on the RDBMS servers to store data.
Figure 43 – The Distributed Computing Revolution aided object-oriented architecture (click to enlarge)
In the late 1990s, the Internet exploded upon the business world and greatly enhanced the 3-tier model of Figure 43. The “thin client” running on PCs now became a web browser like Internet Explorer. Middleware containing business logic was run on Application servers that produced dynamic web pages that were dished up by Web servers like Apache. Data remained back on mainframes or RDBMS servers. Load balancers were also used to create clusters of servers that could scale load. As your processing load increased, all you had to do was buy more servers for each tier in the architecture to support the added load. This opened an ecological niche for the middleware software that ran on the Appserver tier of the architecture. At the time, people were coming up with all sorts of crazy ways to create dynamic HTML web pages on the fly. Some people were using Perl scripts, while others used C programs, but these all required a new process to be spawned each time a dynamic web page was created and that was way too much overhead. Then Java came crashing down like a 10-kilometer wide asteroid! Java, Java, Java – that’s all we heard after it hit in 1995. Java was the first object-oriented programming language to take on IT by storm. The syntax of Java was very nearly the same as C++, without all the nasty tricky things like pointers that made C++ and C so hard to deal with. C++ had evolved from C in the 1980s, and nearly all computer science majors had cut their programming teeth on C or C++ in school, so Java benefited from a large population of programmers familiar with the syntax. The end result was a mass extinction of non-Java-based software on the distributed computing platform and the rapid rise of Java-based applications like an impactor mass extinction. Even Microsoft went Object-Oriented on the Windows server platform with its .NET Framework using its Java-like C# language. Procedural, non-Object Oriented software like COBOL, sought refuge in the mainframes where it still hides today.
Figure 44 – A modern multi-tier website topology (click to enlarge)
For more about software using complex carbon-based multicellar organization see Software Embryogenesis.
SOA - Service Oriented Architecture Period (2004 – 2015)
The next advance in software architecture came as the Service Oriented Architecture (SOA) Period, which was very similar to the Cambrian Explosion. During the Cambrian Explosion, 541 million years ago, complex body plans first evolved, which allowed cells in multicellular organisms to make RMI (Remote Method Invocation) and CORBA (Common Object Request Broker Architecture) calls upon the cells in remote organs to accomplish biological purposes. In the Service Oriented Architecture Period, we used common EJB components in J2EE appservers to create services that allowed for Applications with complex body plans. The J2EE appservers performed the functions of organs like kidneys, lungs and livers. I am discounting the original appearance of CORBA in 1991 here as a failed precursor because CORBA never became ubiquitous as EJB later became. In the evolution of any form of self-replicating information, there are frequently many failed precursors leading up to a revolution in technology.
There is a growing body of evidence beginning to support the geological "Snowball Earth" hypothesis that the Earth went through a period of 100 million years of extreme climatic fluctuations just prior to the Cambrian Explosion. During this period, the Earth seesawed between being completely covered with a thick layer of ice and being a hothouse with a mean temperature of 140 0F. Snowball Earth (2003) by Gabrielle Walker is an excellent book covering the struggles of Paul Hoffman, Joe Kirschvink, and Dan Schrag to uncover the evidence for this dramatic discovery and to convince the geological community of its validity. It has been suggested that the resulting stress on the Earth's ecosystems sparked the Cambrian Explosion. As we saw above, for the great bulk of geological time, the Earth was dominated by simple single-celled organisms. The nagging question for evolutionary biology has always been why did it take several billion years for complex multicellular life to arise, and why did it arise all at once in such a brief period of geological time? As a field geologist works up from pre-Cambrian to Cambrian strata, suddenly the rocks burst forth with complex fossils where none existed before. For many, the first appearance of complex life just following the climatic upheaval of the Snowball Earth is compelling evidence that these two very unique incidents in the Earth’s history must be related.
Similarly for IT, the nagging question is why did it take until the first decade of the 21st century for the SOA Cambrian Explosion to take place when the first early precursors can be found as far back as the mid-1960s? After all, software based upon multicellular organization, also known as object-oriented software, goes all the way back to the object-oriented language Simula developed in 1965, and the ability for objects (cells) to communicate between CPUs arose with CORBA in 1991. So all the precursors were in place nearly 15 years earlier, yet software based upon a complex multicellular architecture languished until it was jarred into existence by a series of harsh environmental shocks to the IT community. It was the combination of moving off the mainframes to a distributed hardware platform, running on a large number of servers and client PCs, the shock of the Internet upon the business world and IT, and the impact of Sun’s Java programming language, that ultimately spawned the SOA (Service Oriented Architecture) Cambrian Explosion. These shocks all occurred within a few years of each other in the 1990s, and after the dust settled, IT found itself in a new world of complexity.
To see how this works, let’s examine more closely the inner workings of a J2EE Appserver. Figure 45 shows the interior of a J2EE Appserver like WebSphere. The WebSphere middleware is software that runs on a Unix server which might host 30 or more WebSphere Appserver instances and there might be many physical Unix servers running these WebSphere Appserver instances in a Cell (Tier). Figure 44 shows a Cell (Tier 2) consisting of two physical Application servers or nodes, but there could easily be 4 or 5 physical Unix servers or nodes in a WebSphere Cell. This allows WebSphere to scale, as your load increases, you just add more physical Unix servers or nodes to the Cell. So each physical Unix server in a WebSphere Cell contains a number of software Appserver instances as shown in Figure 45, and each Appserver contains a number of WebSphere Applications that do things like creating dynamic web pages for a web-based application. For example, on the far left of Figure 45, we see a client PC running a web browser like Chrome. The web browser makes HTTP requests to an HTTP webserver like Apache. If the Apache webserver can find the requested HTML page, like a login page, it returns that static HTML page to the browser for the end-user to fill in his ID and PASSWORD. The user’s ID and PASSWORD are then returned to the Apache webserver when the SUBMIT button is pressed, but now the Apache webserver must come up with an HTML page that is specific for the user’s ID and PASSWORD like a web page with the end-user’s account information. That is accomplished by having Apache forward the request to a WebSphere Application running in one of the WebSphere Appservers. The WebSphere Appserver has two software containers that perform the functions of an organ in a multicellular organism. The Web Container contains instances of servlets and JSPs (Java Server Pages). A servlet is a Java program that contains logic to control the generation of a dynamic web page. JSPs are HTML pages with tags for embedded programming logic that are compiled into servlets at execution time. The servlets in the Web Container create objects and are run in a thread pool in the Web Container, like the cells in a liver or kidney. Unlike the mainframe processing of the Unstructured Period, in which a program was loaded into memory, run, and then perished, these servlets remain in memory and are continuously reused by the thread pool to service additional requests, until no further requests arrive and the servlet is destroyed to make room for another servlet in the thread pool. The EJB Container performs a similar function by running EJBs (Enterprise Java Beans) in a thread pool. The EJBs provide business logic and connect to databases (DB) and mainframes (EIS – Enterprise Information Systems). By keeping the servlets and EJBs running continuously in memory, with permanent connections to databases and mainframes via connection pools, the overhead of loading and releasing the servlets is eliminated as well as the creation and tear-down of connections to databases and mainframes. So the Web and EJB Containers of a J2EE Appserver are very much like the cells in an organ that continuously provide services for the other cells of a multicellular organism. Look at it this way, unlike a simple single-celled organism that is born, lives, and dies, your body consists of 100 trillion cells and each day about a trillion cells die and are replaced by a trillion new cells, but through it all you keep going. A simple single-celled organism is like a batch program from the Unstructured Period, while your body runs on a SOA architecture of trillions of cells in thread and connection pools that are constantly coming and going and creating millions of objects that are created (instantiated), used, and later destroyed.
Figure 45 - A J2EE Application Server contains a WEB Container that stores pools of Servlet Objects and an EJB Container that stores pools of EJB Objects. The EJB Objects get data from relational databases (DB) and processes the data and then passes the information to Servlet Objects. The Servlet Objects generate HTML based upon the data processed by the EJB Objects and pass the HTML to HTTP webservers like Apache.
For more about complex multicellular software built on SOA architecture see Software Embryogenesis.
Design Patterns – the Phyla of IT
Another outgrowth of the object-oriented programming revolution was the adoption of design patterns by IT. Design patterns originated as an architectural concept developed by Christopher Alexander in the 1960s. In Notes on the Synthesis of Form (1964), Alexander noted that all architectural forms are really just implementations of a small set of classic design patterns that have withstood the test of time in the real world of human affairs and that have been blessed by the architectural community throughout history for both beauty and practicality. Basically, given the physical laws of the Universe and the morphology of the human body, there are really only a certain number of ways of doing things from an architectural point of view that work in practice, so by trial and error architects learned to follow a set of well established architectural patterns. In 1987, Kent Beck and Ward Cunningham began experimenting with the idea of applying the concept of design patterns to programming and presented their results at the object-oriented OOPSLA conference that year. Design patterns gained further popularity in computer science after the book Design Patterns: Elements of Reusable Object-Oriented Software was published in 1994 by Erich Gamma, Richard Helm, and Ralph Johnson. Also in 1994, the first Pattern Languages of Programming Conference was held, and in 1995 the Portland Pattern Repository was established to document design patterns for general IT usage.
However, the concept of design patterns goes back much further than this. In biology, a design pattern is called a phylum, which is a basic body plan. For example, the phylum Arthropoda consists of all body plans that use an external skeleton such as the insects and crabs, and the Echinodermata have a five-fold radial symmetry like a starfish. Similarly, the phylum Chordata consists of all body plans that have a large dorsal nerve running down a hollow backbone or spinal column. The Cambrian Explosion, 541 million years ago, brought about the first appearance of a large number of phyla or body plans on Earth. In fact, all of the 35 phyla currently found on the Earth today can trace their roots back to the Cambrian, and it even appears that some of the early Cambrian phyla have gone completely extinct, judging by some of the truly bizarre-looking fossils that have been found in the Burgess Shale of the highly experimental Cambrian period.
In IT a design pattern describes a certain design motif or way of doing things. A design pattern is a prototypical design architecture that developers can copy and adapt for their particular application to solve the general problem described by the design pattern. This is in recognition of the fact that at any given time there are only a limited number of IT problems that need to be solved at the application level, and it makes sense to apply a general design pattern rather than to reinvent the wheel each time. Developers can use a design pattern by simply adopting the common structure and organization of the design pattern for their particular application, just as living things adopt an overall body plan or phylum to solve the basic problems of existence. In addition, design patterns allow developers to communicate with each other using well-known and well-understood names for software interactions, just as biologists can communicate with each other by using the well-known taxonomic system of classification developed by Carl Linnaeus in Systema Naturae published in 1735.
A design pattern that all Internet users should be quite familiar with is the Model-View-Controller (MVC) design pattern used by most web-applications. Suppose you are placing an order with Amazon. The Model is the data that comprises your Amazon account information, such as your credit card number on file and your mailing address, together with all the items in your shopping cart. In Figure 45 above, the Model is stored on a relational database server DB, such as an Oracle server, or back on a mainframe in an EIS (Enterprise Information System) connected to a mainframe DB2 database as a series of relational database tables. The View is the series of webpages presented to your browser as .html pages that convey the Model data to you in a sensible form as you go about your purchase. These View .html pages are generated by JSPs (Java Server Pages) in the web container of the J2EE Appserver. The Controller is a servlet, a java program running in a thread pool in the web container of the J2EE Appserver, that performs the overall control of your interactions with the Amazon application as you go about placing your order. The Controller servlet calls JSPs and instantiates objects (cells) that call EJB objects (cells) in the EJB container of the J2EE Appserver that interact with the relational database tables storing your data.
During the first decade of the 21st century, the Service Oriented Architecture rapidly expanded in the IT community and began to expand beyond the traditional confines of corporate datacenters, as corporations began to make services available to business partners over the Internet. With the flexibility of Service Oriented Architecture and the Internet, we began to see the evolution of an integrated service-oriented ecology form - a web of available services like the web of life in a rain forest. Today, we call that rain forest ecology of shared software services over the Internet the Cloud Microservices Platform.
Cloud Computing and the Rise of the Cloud Computing Microservices of Today
The age of Cloud Microservices marks the latest period of software evolution. Cloud Computing allows developers to spend less time struggling with the complexities of the Distributed Computing Platform that first arose in the 1990s. Cloud Microservices allow developers to build new applications by stitching together Cloud-based Microservices running in Cloud containers in the Cloud. This seems to be the next wave of the future for IT. The use of Microservices is another emerging technology in Cloud computing that extends our experiences with SOA. SOA (Service Oriented Architecture) arrived in 2004. With SOA, people started to introduce common services in the Middleware layer of the three-tier Distributed Computing Model. SOA allowed other Middleware application components to call a set of common SOA services for data. That eliminated the need for each application to reinvent the wheel each time for many common application data needs. Cloud Microservices take this one step further. Instead of SOA services running on bare-metal Unix servers, Cloud Microservices run in Cloud Containers and each Microservice provides a very primitive function. By using a large number of Cloud Microservices running in Cloud Containers, it is now possible to quickly throw together a new application and push it into Production.
So before concluding, I would like to relay some of my experiences with the power of something like Cloud Microservices. I left Amoco in 1999 when BP bought Amoco and terminated most of Amoco's IT Department. For more on that see Hierarchiology and the Phenomenon of Self-Organizing Organizational Collapse. I then joined the IT Department of United Airlines working on the CIDB - Customer Interaction Data Base. The CIDB initially consisted of 10 C++ Tuxedo services running in a Tuxedo Domain on Unix servers. Tuxedo (Transactions Under Unix) was an early form of Middleware software developed in the 1980s to create a TPM (Transaction Processing Monitor) running under Unix that could perform the same kind of secured transaction processing that IBM's CICS (1968) provided on IBM MVS mainframes. The original 10 Tuxedo services allowed United's business applications and the www.united.com website to access the data stored on the CIDB Oracle database. We soon found that Tuxedo was very durable and robust. You could literally throw Tuxedo down the stairs without a dent! A Tuxedo Domain was very much like a Cloud Container. When you booted up a Tuxedo Domain, a number of virtual Tuxedo servers were brought up. We had each virtual Tuxedo server run just one primitive service. The Tuxedo Domain had a configuration file that allowed us to define each of the Tuxedo servers and the service that ran in it. For example, we could configure the Tuxedo Domain so that a minimum of 1 and a maximum of 10 instances of Tuxedo Server-A were brought up. So initially, only a single instance of Tuxedo Server-A would come up to receive traffic. There was a Tuxedo queue of incoming transactions that were fed to the Tuxedo Domain. If the first instance of Tuxedo Service-A was found to be busy, a second instance of Tuxedo Server-A would be automatically cranked up. The number of Tuxedo Server-A instances would then dynamically change as the Tuxedo load varied. Like most object-oriented code, the C++ code for our Tuxedo services had memory leaks, but that was not a problem for us. When one of the instances of Tuxedo Server-A ran out of memory, it would simply die and another instance of Tuxedo Service-A would be cranked up by Tuxedo. We could even change the maximum number of running Tuxedo Service-A instances on the fly without having to reboot the Tuxedo Domain.
United Airlines found the CIDB Tuxedo Domain to be so useful that we began to write large numbers of Tuxedo services. For example, we wrote many Tuxedo services that interacted with United's famous Apollo reservation system that first appeared in 1971, and also with many other United applications and databases. Soon United began to develop new applications that simply called many of our Tuxedo Microservices. We tried to keep our Tuxedo Microservices very atomic and simple. Rather than provide our client applications with an entire engine, we provided them with the parts for an engine, like engine blocks, pistons, crankshafts, water pumps, distributors, induction coils, intake manifolds, carburetors and alternators.
One day in 2002 this came in very handy. My boss called me into his office at 9:00 AM one morning and explained that United Marketing had come up with a new promotional campaign called "Fly Three - Fly Free". The "Fly Three - Fly Free" campaign worked like this. If a United customer flew three flights in one month, they would get an additional future flight for free. All the customer had to do was to register for the program on the www.united.com website. In fact, United Marketing had actually begun running ads in all of the major newspapers about the program that very day. The problem was that nobody in Marketing had told IT about the program and the www.united.com website did not have the software needed to register customers for the program. I was then sent to an emergency meeting of the Application Development team that supported the www.united.com website. According to the ads running in the newspapers, the "Fly Three - Fly Free" program was supposed to start at midnight, so we had less than 15 hours to design, develop, test and implement the necessary software for the www.united.com website! Amazingly, we were able to do this by having the www.united.com website call a number of our primitive Tuxedo Microservices that interacted with the www.united.com website and the Apollo reservation system.
The use of many primitive Microservices is also extensively used by carbon-based life on this planet. In Facilitated Variation and the Utilization of Reusable Code by Carbon-Based Life, I showcased the theory of facilitated variation by Marc W. Kirschner and John C. Gerhart. In The Plausibility of Life (2005), Marc W. Kirschner and John C. Gerhart present their theory of facilitated variation. The theory of facilitated variation maintains that, although the concepts and mechanisms of Darwin's natural selection are well understood, the mechanisms that brought forth viable biological innovations in the past are a bit wanting in classical Darwinian thought. In classical Darwinian thought, it is proposed that random genetic changes, brought on by random mutations to DNA sequences, can very infrequently cause small incremental enhancements to the survivability of the individual, and thus provide natural selection with something of value to promote in the general gene pool of a species. Again, as frequently cited, most random genetic mutations are either totally inconsequential, or totally fatal in nature, and consequently, are either totally irrelevant to the gene pool of a species or are quickly removed from the gene pool at best. The theory of facilitated variation, like classical Darwinian thought, maintains that the phenotype of an individual is key, and not so much its genotype since natural selection can only operate upon phenotypes. The theory explains that the phenotype of an individual is determined by a number of 'constrained' and 'deconstrained' elements. The constrained elements are called the "conserved core processes" of living things that essentially remain unchanged for billions of years, and which are to be found to be used by all living things to sustain the fundamental functions of carbon-based life, like the generation of proteins by processing the information that is to be found in DNA sequences, and processing it with mRNA, tRNA and ribosomes, or the metabolism of carbohydrates via the Krebs cycle. The deconstrained elements are weakly-linked regulatory processes that can change the amount, location and timing of gene expression within a body, and which, therefore, can easily control which conserved core processes are to be run by a cell and when those conserved core processes are to be run by them. The theory of facilitated variation maintains that most favorable biological innovations arise from minor mutations to the deconstrained weakly-linked regulatory processes that control the conserved core processes of life, rather than from random mutations of the genotype of an individual in general that would change the phenotype of an individual in a purely random direction. That is because the most likely change of direction for the phenotype of an individual, undergoing a random mutation to its genotype, is the death of the individual.
Marc W. Kirschner and John C. Gerhart begin by presenting the fact that simple prokaryotic bacteria, like E. coli, require a full 4,600 genes just to sustain the most rudimentary form of bacterial life, while much more complex multicellular organisms, like human beings, consisting of tens of trillions of cells differentiated into hundreds of differing cell types in the numerous complex organs of a body, require only a mere 22,500 genes to construct. The baffling question is, how is it possible to construct a human being with just under five times the number of genes as a simple single-celled E. coli bacterium? The authors contend that it is only possible for carbon-based life to do so by heavily relying upon reusable code in the genome of complex forms of carbon-based life.
Figure 46 – A simple single-celled E. coli bacterium is constructed using a full 4,600 genes.
Figure 47 – However, a human being, consisting of about 100 trillion cells that are differentiated into the hundreds of differing cell types used to form the organs of the human body, uses a mere 22,500 genes to construct a very complex body, which is just slightly under five times the number of genes used by simple E. coli bacteria to construct a single cell. How is it possible to explain this huge dynamic range of carbon-based life? Marc W. Kirschner and John C. Gerhart maintain that, like complex software, carbon-based life must heavily rely on the microservices of reusable code.
Conclusion
This concludes our walk through the 2.6 billion seconds of software and hardware evolution in Deep Time. Please note that it took the IT community about 2.6 billion seconds to develop the Cloud-based Microservices Architecture of today that is based upon multicellular organization. This was achieved through the very slow Darwinian processes of inheritance, innovation and natural selection and was performed by many millions of independently acting programmers. Granted, this occurred much faster than the four billion years that nature took to come up with the same architecture, but we could have done this back in the 1960s if we had only known better – after all, the object-oriented language Simula was developed in 1965. Softwarephysics proposes that we learn from biology to quickly skip to solutions directly. Still, given that software and hardware met these conditions:
1. Each system is formed from numerous interacting units (e.g., nuclear particles, chemical elements, organic molecules, or cells) that result in combinatorially large numbers of possible configurations.
2. In each of these systems, ongoing processes generate large numbers of different configurations.
3. Some configurations, by virtue of their stability or other “competitive” advantage, are more likely to persist owing to selection for function.
The modern IT world of today became inevitable:
The Law of Increasing Functional Information:
The Functional Information of a system will increase (i.e., the system will evolve) if many different configurations of the system are subjected to selection for one or more functions.
Comments are welcome at
scj333@sbcglobal.net
To see all posts on softwarephysics in reverse order go to:
https://softwarephysics.blogspot.com/
Regards,
Steve Johnston





























